Chapitre 2 : suivi temporel d’une réaction chimique

Étude cinétique par conductimétrie

Q1

a) Demi-équations électroniques pour chacun des deux couples qui interviennent dans cette réaction.

S₂O₈^2- + 2 e^- = 2 SO₄^2-

½ réaction de réduction car gain d’électrons

2I^- = I₂ + 2 e^-

½ réaction d’oxydation car perte d’électrons

b) Réaction entre les ions peroxodisulfate et les ions iodure.

S₂O₈^2- + 2I^- = 2 SO₄^2- + I₂

c) Les quantités de matière sont exprimées en mole

Relation stœchiométrique		2I^– (aq) + S2O8^2–(aq) = I2 (aq) + 2 SO4^2–(aq)
État du système	Avancement	Quantité de matière en mol
État initial	x = 0	C2V2 = 1,5x10^-1x60x10^-3 = 90x10^-4	C1V1 = 40x10^-3x10^-1 =40x10^-4	0	0
Au cours de la transformation	x	90x10^-4 – 2x	40x10^-4 – x	x	2x
État final attendu	xmax	90x10^-4 – 2xmax = 10x10^-4	40x10^-4 – xmax = 0	xmax = 40x10^-4	2xmax = 80x10^-4 mol

Calcul de x_max

90x10^-4 – 2x_max = 0 ; x_max = 45x10^-4 mol

40x10^-4 – x_max = 0 ; x_max = 40x10^-4 mol

Conclusion : x_max = 40x10^-4 mol ; le réactif en défaut est le peroxodisulfate.

d) Vidéo

V =V₁ + V₂

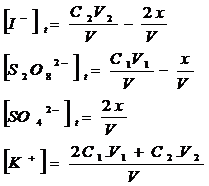
Q2

Vidéo

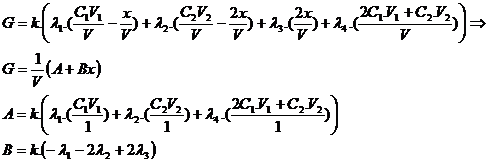
Q3

a) Vidéo

La vitesse volumique 'v(t)' d'une réaction calculée à l'instant 't' est égale à la dérivée de l'avancement 'x' par rapport au temps, divisée par le volume V de solution  :

Unité légale : mol.s^-1m^-3.

b) Vidéo

G= (1/V).(A + Bx)

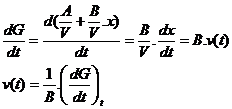
c) Vidéo

Valeur v_o de la vitesse volumique à la date t = 0 s (début de réaction).

Calcul de (dG/dt)_{t = 0}

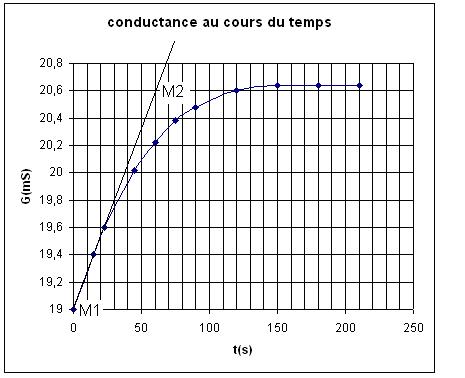
1) on trace la tangente à la courbe à l’instant t = 0 ;

2) on prend 2 points de cette tangente

M1 ( t1 = 0 s ; G1 = 19 mS) ; M2 (t2 = 60 s , G2 = 20,6 mS)

3) on calcule la pente qui est égale à (dG/dt)_{t = 0}

4) On calcule v(o)

Q4

a) Le temps de demi-réaction est la durée au bout de laquelle l'avancement est égal à l'avancement final divisée par 2 :

Dans le cas où la réaction est totale, x_f = x_max par conséquent le temps de demi-réaction est la durée au bout de laquelle l'avancement est égal à la moitié de l'avancement maximal :

b) G= (1/V).(A + Bx)

*A t = 0 x =0 donc Go = A/V or A = 1,9 mS.L et V =100 mL = 0,1L

Go = A/V = 1,9/0,1 = 19 mS . Sur le graphique on lit qu’à t = 0, Go = 19 mS, les 2 valeurs sont identiques ouf !

* A la fin de la réaction, Gmax= (1/V).(A + Bx_max) = (1/0,1)x(1.9+42x40x10^-4) = 20,7 mS

Sur le graphique on lit sensiblement la même valeur.

c) Vidéo

G_1/2 = (1/V).(A + Bx_max/2) = Go + (B/V).(x_max/2)

Gmax = Go + (B/V). max

x_max = (Gmax – Go).(V/B)

G_1/2 = Go +1/2.(Gmax – Go)

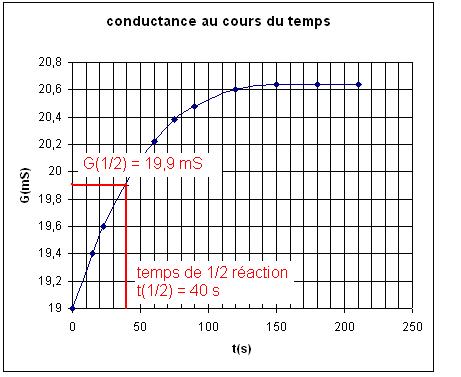
d) G_1/2 = Go +1/2.(Gmax – Go) = 19 + ½ (20,7 – 19) = 19,9 mS

D’après le graphique t(1/2) = 40 s

e) Vidéo

La valeur de x_max ne change pas, donc celle de Gmax non plus. Seule la vitesse augmente. Or la vitesse est proportionnelle à la pente de la tangente à la courbe G = f(t) car :

Donc la pente de la tangente à la courbe est plus importante en chaque instant. Allure de la courbe :