Quelques propriétés des solutions
de nitrate d’argent et d’ammoniac ( Pondichéry 2007 ; 7 points)
On donne quelques valeurs :
|
Conductivités molaires ioniques des ions à |
||
|
Ion ammonium |
Ion hydroxyde |
Ion oxonium |
|
NH4+(aq) |
HO –(aq) |
H3O+(aq) |
|
7,4 |
19,8 |
35,0 |
§ Masses molaires
atomiques : M(Ag) =
§ Valeur de la
constante de Faraday : NA.e = 9,65 ´ 104
C.mol-1 (NA est la constante d’Avogadro et e la charge
élémentaire).
I.1. - Constante
d’acidité du couple ion ammonium / ammoniac (NH4+(aq)
/ NH3(aq))
On dissout du gaz ammoniac dans de l’eau : on obtient une solution
(S).
I.1.1 - NH3(aq) + H2O(l) = NH4+(aq) + HO–(aq)
I.1.2 - La solution (S) est
une solution basique selon Bronsted car elle capte un ion H+ de
l’acide H20.
I.1.3
-
Expression de la conductivité d’une solution d’ammoniac en fonction des conductivités molaires ioniques des
espèces en solution et de leurs concentrations molaires volumiques.
=
l(NH4+(aq)).[NH4+(aq)]éq + l(HO-(aq)).[HO-(aq)]éq
I.1.4
– Vidéo
![]()
![]()
NH3(aq) + H2O(l) = NH4+(aq) + HO–(aq)
![]() =
= ![]() (NH4+(aq)).[NH4+(aq)]éq +
(NH4+(aq)).[NH4+(aq)]éq + ![]() (HO-(aq)).[HO-(aq)]éq
(HO-(aq)).[HO-(aq)]éq
A l’équilibre : [NH4+(aq)] =
[ HO–(aq)] = xeq/V
![]()
![]()
I.1
.5 – Vidéo
Concentration
molaire effective des ions oxonium et des molécules d’ammoniac NH3.
![]() avec cO = 1,0
mol.L-1
avec cO = 1,0
mol.L-1![]()
A
l’équilibre d’après l’équation bilan:
[NH3(aq) ]éq = [NH3(aq)
]i –xeq/V
[NH3(aq) ]éq =
[NH3(aq) ]i –[NH4+(aq)]éq = 1,00×10–2 – 4,0×10–4 =
9,6×10–3 mol.L-1
I.1.6 –Vidéo
Expression de la constante d’acidité du couple ion
ammonium/ammoniac :
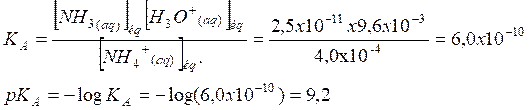
L’énoncé donne
pour valeur de pKA = 9,24 : les 2 valeurs sont similaires
obtenue est compatible.
I.2.- Nitrate
d’argent et cuivre.
I.2.1.a- Demi-équations
associées aux réactions d’oxydation et de réduction qui se sont produites. :
Cu(s) = Cu2+(aq) + 2 e– Oxydation (×1) car
perte d’électrons
Ag+(aq) + e– = Ag(s)
Réduction (×2) car gain d’électrons
I.2.1.b- Equation de la
réaction d’oxydoréduction entre le cuivre et les ions argent (I).
. Cu(s) + 2Ag+(aq) = Cu2+(aq)
+
2 Ag(s)
I.2.2 - Pile cuivre
argent
I.2.2.a – Vidéo
Schéma  légendé de la pile
légendé de la pile
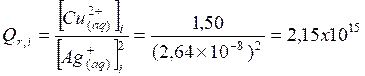
Qr, i = K, le système chimique est dans son état
d’équilibre : l’avancement est nul , la pile ne
peut pas débiter de courant.
I.2.2.b
– Voir schéma ci contre.
Les porteurs de
charge à l’intérieur de la pile sont :
- les cations NH4+
Cu2+ et Ag+ qui se
déplacent dans le sens du courant électrique
- les anions NO3- , SO42-
dans le sens opposé (voir schéma ci contre).
I.2.2.c – Vidéo
Cu2+(aq) + 2 e–
= Cu(s) Réduction
(×1)
Ag(s) =
Ag+(aq) + e– Oxydation (×2)
Cu2+(aq) + 2 Ag(s) = Cu(s)
+ 2Ag+(aq)
I.2.2.d
- Établir le tableau descriptif de l’évolution du système :
1. Tout est en mole !
|
Équation |
Cu2+(aq) + 2 Ag(s) = Cu(s) + 2 Ag+(aq) |
|||
|
État
initial (en mol) |
ni(Cu2+(aq)) = 3,00´10–2 |
ni(Ag(s)) = 2,5´10–2 |
ni(Cu(s)) = 1,73´10–1 |
ni(Ag+(aq)) = 5,28x10-10
(négligeable) |
|
État
pour un avancement x (en mol) |
ni(Cu2+(aq)) – x |
ni(Ag(s)) – 2x |
ni(Cu(s)) + x |
2x |
ni(Cu2+(aq))
= [Cu2+(aq))]i.V ni(Cu2+(aq)) = 1,50×20,0×10–3 = 3,00×10–2
mol
Attention seule la
moitié des plaques plongent dans les solutions : on ne considère
alors que la moitié de leur masse pour les calculs des quantités de matière.
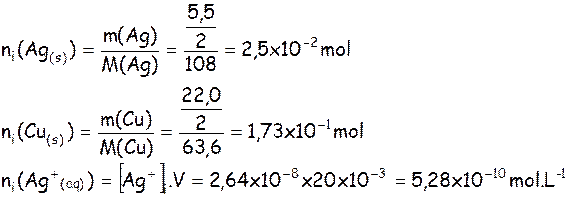
I.2.2.e
-
. Vidéo
Pour effectuer ce calcul
écrire l’équation bilan de la réaction et non pas la ½ équation qu’on oublie de
coefficienter !
Cu(s) + 2Ag+(aq) + 2e- = Cu2+(aq)
+
2 Ag(s) + 2e-
I = 150 mA; t = 1h
D’après les
nombres stœchiométriques de l’équation bilan la quantité de matière d’électrons
n(e-) = 2x .La quantité d’électricité
correspondante est:
Q = n(e–).NA.e = 2 x.NA.e
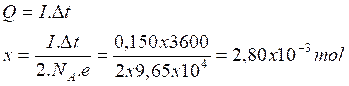
I.2.2.f – D’après le
tableau d’avancement :
|
État
pour un avancement x (en mol) |
ni(Cu2+(aq)) – x |
ni(Ag(s)) – 2x |
ni(Cu(s)) + x |
2x |
[Ag+(aq)]1h = 2x/V = (2x2,80x10-3)/(20x10-3)
= 2,80x10-1 mol.L-1
[Cu2+(aq)]1h = (ni(Cu2+(aq)) – x)/V = (3,00x10-2 -2,80x10-3)/(20x10-3)
= 1,36 mol.L-1