Chapitre 2 : Magnétostatique
ENAC 2003 énoncé
Q1
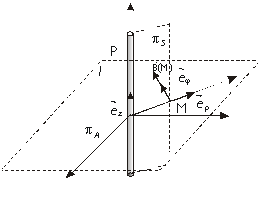
Une symétrie par rapport au plan
P1, perpendiculaire au fil et passant par le point M d'observation
transforme I en -I donc 
reste
inchangé : Il appartient au plan P1.
Si l'on fait une symétrie par
rapport au plan contenant le fil et
passant par M, I reste invariant donc 
est perpendiculaire à P2.
On
en déduit donc que 
est orthoradial : 
Toute
translation suivant l'axe Oz ne modifie pas le problème donc B(M) est indépendant de z. Toute rotation d'angle
q
ne modifie pas le problème donc B(M) est indépendant de q. 
On cherche un contour sur lequel la circulation de 
se ramène à un simple produit non nul.Or, B
est constant sur une courbe d'équation 
= cte : On choisit donc un cercle de rayon r
Attention, tout contour doit être orienté pour pouvoir
calculer le flux de 
:
= 
.
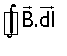D'où 
: Réponse a)
Q2
La force élémentaire exercée sur le fil est 
d’où 
:
Réponse a)
Q3
La force élémentaire exercée sur le fil est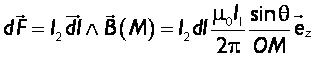 
La résultant suivant 
est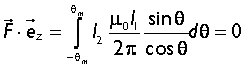 
. La résultant suivant est nulle : Réponse b)
Q4
La résultante ne dépend pas de h donc 
:
Réponse b)