Chapitre 10 : chute libre

RECHERCHE D’UN MODÈLE DE FORCE DE FROTTEMENT

Recherche d’un modèle de force de frottement (2005 Réunion)

A. Exploitation de l’enregistrement

A-1.(0,5 pt)

M15	300	211,0	0,95
M16	320	231,0	0,95
M17	340	249,0	0,95
M18	360	269,0	0,95
M19	380	287,0	0,95
M20	400	307,0	0,95

D’après le document 1, la trajectoire de la bille est une droite. D’après le document 2, la vitesse entre M₁₅ et M₂₁ est constante.

Le mouvement de la bille est un mouvement rectiligne uniforme.

D’après la première loi de Newton ou principe d'inertie si le vecteur vitesse du centre d’inertie est constant alors dans cette portion de mouvement la somme des forces extérieures agissant sur la bille est nulle.

A-2. (0,5 pt)L’intervalle de temps entre 2 positions successives est de 20 ms, en effet la caméra prend 50 images par secondes Entre 2 images il s’écoule une durée :

1/50 = 0,02 s = 20 ms

.

B. Étude cinématique

B-1. (0,5 pt, 0,25 + 0,25)Vitesse au point M6 :

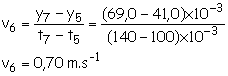
B-2. (0,5 pt, 0,25 + 0,25)Comme les vecteurs vitesses ont même direction et le même sens, on utilise pour le calcul de la norme la relation :

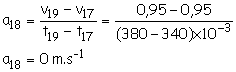
Le résultat obtenu est compatible avec la question A-1. En effet le mouvement est rectiligne uniforme à partir du point M₁₅ . La somme des forces extérieures est nulle donc le vecteur accélération est nulle :

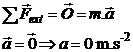
C. Étude dynamique

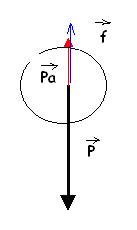
C-1. (0,75 pt, 0,25 + 0,25+0,25) Dans un référentiel terrestre, supposé galiléen, la bille est soumise à l’action de 3 forces de direction verticale :

.

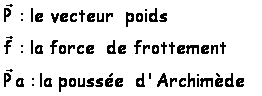
C-2. (0,5 pt, 0,25+0,25) Masse m de la bille :

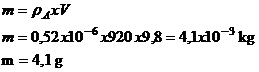
C-3. (0,5 pt, 0,25+0,25)Calcul de la poussée d’Archimède :

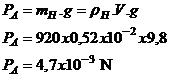
D. Équation différentielle du mouvement de la bille

D-1. (1 pt, 0,5+0,5) Deuxième loi de Newton  : dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide de masse m, est égale au produit de cette masse par le vecteur accélération de son centre d’inertie :

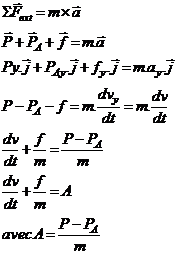
D-2. (0,5 pt, 0,25+0,25)Calcul de la valeur de A :

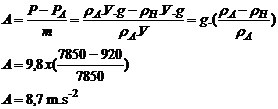
D’après l’expression précédente A à pour unité le m.s^{-2 .} le rapport des masse volumique est sans unité et l’unité de g est le m.s^-2.

E. Recherche de modèles pour la force de frottement

E-1. Première hypothèse : f = k₁.v

E-1.a) (0,5 pt ) f = k₁.v par conséquent l’équation différentielle devient :

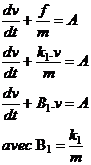
E-1.b) (0,5 pt, 0,25+0,25) Quand la vitesse limite est atteinte, la valeur de la vitesse est constante. Par conséquent :

dv/dt = 0. On reporte dans l’équation différentielle la valeur de v = v_lim :

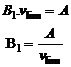
E-2. (0,25 pt) f = k₂.v² . De la même façon que dans l’exercice précédent, lorsque la vitesse limite est atteinte dv/dt = 0.

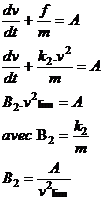
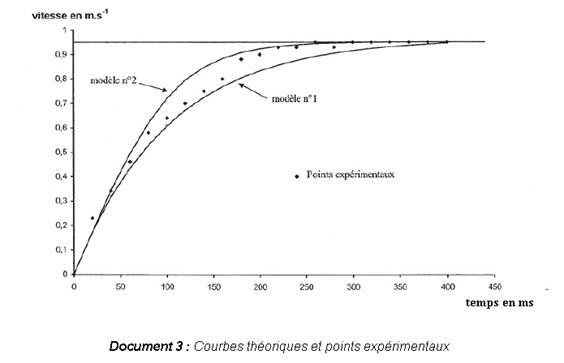
E-3. (0,5 pt)

Pour 0 v 0,8 m.s^–1, il semble que le modèle 1 convienne mieux car la courbe expérimentale s’en rapproche d’avantage.

.

Pour 0,8 v 1 m.s^–1, il semble que ce soit le modèle 2 qui convienne le mieux.