Chapitre 2 : le microscope

 

Microscope classique et microscope confocal (métropole 09/06 )

 

1. Étude d'un microscope optique classique

 

1.1. Position de l'image intermédiaire A1B1

 

1.1.1          Image intermédiaire A1B1 de l'objet AB.

1.1.2          Formule de conjugaison des lentilles minces (relation de Descartes).

 

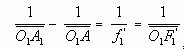
1.2. Observation de l'objet à travers le microscope

1.2.1.        A1B1 est un objet pour l’oculaire L2. (vidéo)

1.2.2.        A1B1 doit se trouver dans le plan focal objet de la lentille pour que son image soit rejetée à l’infini. (vidéo)

1.2.3.        Voir figure ci dessus. (vidéo)

1.2.4.        Position de A par rapport à O1.

 

 

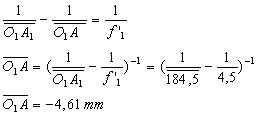
1.3. Calcul du grandissement

 

1.3.1.        Rappeler la formule définissant le grandissement pour la lentille mince (L1) dans le cas étudié. Déterminer sa valeur.

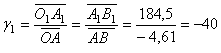
1.3.2.        En s'aidant de la figure 1, montrer que le grandissement g1 de l'objectif peut s'écrire .

D’après la figure 1 :

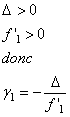
1.3.3.        Que peut-on dire de l'inscription " ´ 40" inscrite sur la monture de l'objectif ?

 

 

Il s’agit de la valeur absolue du grandissement de l’objectif.

 

1.3.4 Position et taille d’ du cercle oculaire

 

 


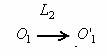
La relation de conjugaison appliquée à la lentille L2 donne :

 

 

 

 

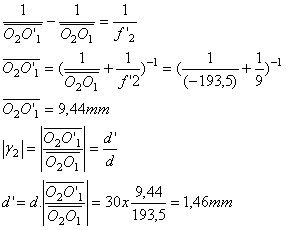
2. Étude du microscope confocal

 

2.1.1          Image du point B

Le rayon passant par O1 n’est pas dévié, le rayon parallèle à l’axe optique converge en passant par F’1.  Le point d’intersection de ses 2 rayons est le point B1

2.1.2          L'image D1 du point D et le faisceau lumineux issu du point D limité par les bords de la lentille.

Construction à partir des 2 mêmes rayons issus de D (rayon parallèle à l’axe optique et passant par le centre optique)

 

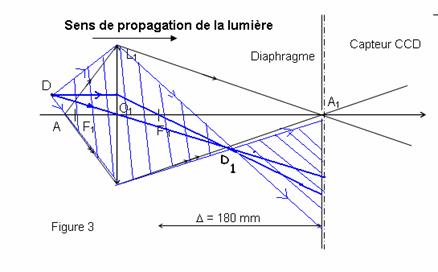
2.1.3 Au vue de la position de l’ouverture du diaphragme (centrée sur l’axe optique) on  voit que seuls les rayons issus du point A arrivent sur le capteur CCD (voir les 2 figures précédentes).

 

2.2. Il faut déplacer l’objet suivant l’axe yy’ vers le bas de manière à ce que le point B se trouve à la place initiale du point A.

 

2.3. Il faut déplacer le point D sur l’axe xx’ vers la droite puis sur l’axe yy’ vers le bas de manière à placer le point D sur la position initiale du point A.