Illustration extraite du logiciel
Solstice
Dans le cas général, la trajectoire est plane;
c'est une ellipse, dont l'un des foyers est le centre de la Terre. Elle présente
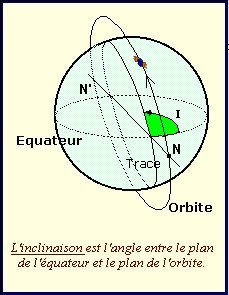
deux points d'intersection avec le plan de l'équateur :
- le nœud ascendant N, qui correspond au passage de l'hémisphère
sud vers l'hémisphère nord,
- le nœud descendant qui correspond au passage de l'hémisphère nord à
l'hémisphère sud.
Cinq paramètres sont alors nécessaires pour
déterminer une orbite elliptique unique, et un autre paramètre permet de déterminer une
position initiale. Les paramètres généralement retenus sont :
Le demi-grand axe, et l'excentricité
qui déterminent la forme de l'ellipse.
Selon la troisième loi de Kepler, la période orbitale est liée uniquement au demi-grand
axe.
L'excentricité e, nulle dans le cas limite d'un cercle, est comprise entre 0 et 1 pour
une ellipse.
Le couple de valeurs demi-grand axe et excentricité donne la forme de l'ellipse et fixe
en particulier les altitudes au périgée (point de la trajectoire le plus près de la
Terre) et à l'apogée (point de la trajectoire le plus éloigné de la Terre).
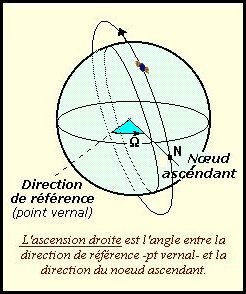
L'ascension droite du noeud ascendant,
qui détermine l'orientation de l'axe des nœuds par rapport à une direction de
référence (point vernal). En pratique, on positionne souvent le plan de l'orbite à
partir de la longitude du noeud ascendant, à une date donnée (ce qui revient à fixer
l'orientation du plan orbital par rapport à l'axe vernal).
L'inclinaison de l'orbite qui est
l'angle entre le plan équatorial et le plan orbital.
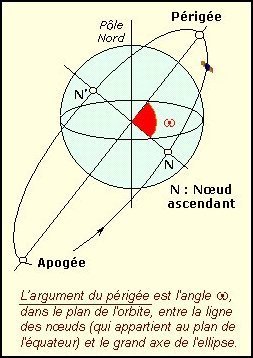
L'argument du périgée qui donne la
position de l'axe de l'ellipse par rapport au plan équatorial.
Il s'agit de l'angle, dans le plan de l'orbite, entre la ligne des nœuds (qui
appartient au plan de l'équateur) et le grand axe de l'ellipse.
|
|
Pour prédire la position du satellite sur
cette orbite à un instant donné, il faut encore connaître sa position à une date de
référence. En pratique, la connaissance de l'heure de passage au nœud ascendant
permet de définir une position initiale, indispensable pour les prédictions
ultérieures.
Cas d'une orbite
circulaire... |