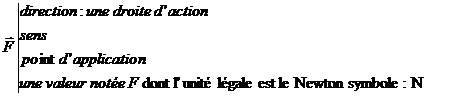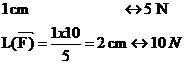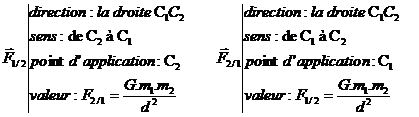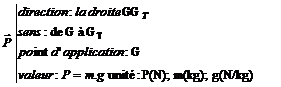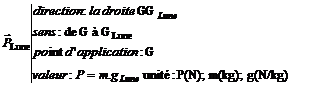Chapitre 8 : la gravitation universelle

Introduction : Toutes les planètes du système solaire gravitent autour du soleil : Leur mouvement est régit par la gravitation universelle. La gravitation universelle est une interaction attractive entre tous les corps de l’univers.

I. les forces d’interaction gravitationnelle

1. Modélisation d’une action par un vecteur force : Vidéo

Une action mécanique est modélisée en physique par un vecteur force. Les 4 caractéristiques du vecteur force sont :

On peut mesurer la valeur d’une force avec un dynamomètre.

Animation : forces s’exerçant sur les avions

Q1 : animation: dynamomètre

Suspendez une masse m = 200 g au bout d’un dynamomètre et donner les 4 caractéristiques de la force de tension de valeur F.

Réponse:

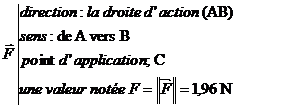2. échelle de représentation d'un vecteur force

Pour représenter un vecteur force il faut choisir une échelle adaptée à la valeur de la force, de manière à ce que le vecteur ne soit ni trop grand ni trop petit!

Exemple: si la valeur de la force est F = 10 N on prendra comme échelle 1 cm représente 5 N

La longueur du vecteur force sera:

Le vecteur mesure 2 cm de long car sa valeur est de 10 N.

3. loi d’interaction gravitationnelle entre deux corps vidéo

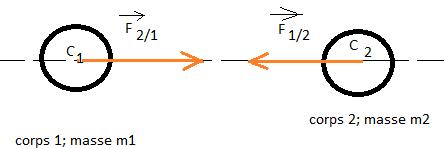
Deux corps 1 et 2 de centres de gravité C₁ et C₂ et de masses m1 et m2 sont éloignés l’un de l’autre d’une distance d = C₁C₂. Le corps 1 exerce sur le corps 2 une force attractive de valeur F_2/1. De même d'après le principe d'interaction le corps 2 exerce sur le corps 1 une force de même valeur notée F_1/2. e valeur). Les 2 forces ont les mêmes valeurs mais des sens opposés : ont dit que les vecteurs forces sont opposés:

Les 4 caractéristiques des vecteurs forces sont:

G= 6,67x10^-11 SI (unité du système international est appelée constante de gravitation

d = C₁C₂ : distance séparant les masses m₁ et m₂ est en mètre(m)

F_1/2 et F_2/1ont pour unité le Newton ; les masses sont exprimées en kg ;

4. Exemple

Q2 : Calculer la force de gravitation s’exerçant sur deux masses ponctuelles de 10,0 g séparées d’une distance de 5,00 cm.

Conclusion : si les corps ont une masse faible les forces d’interaction gravitationnelles sont faibles.

Q3 : cliquer sur l’animation suivante : mouvement des satellites et des planètes puis cliquer sur mouvement des planètes telluriques et gazeuses. Pourquoi les planètes tournent-elles autour du soleil ? Exprimer la valeur de la force d’interaction gravitationnelle du soleil sur Mars et de Mars sur le soleil sans les calculer.

II. poids d’un corps

1. étude expérimentale

Q4 Suspendez à un ressort des masses m différentes. A quoi est égale La force de tension T dont la valeur s’affiche sur le dynamomètre ? Remplir le tableau suivant et en déduire la relation entre le poids d’un objet noté P et sa masse m. On rappelle que l’unité légale de masse est le kilogramme et que 1 g = 10^-3 kg.

Masse m (kg)	0 ,100	0,150	0,200	0,250
Poids P(N)
Rapport P/m

2. le vecteur poids d’un corps sur Terre vidéo

Tous corps, de masse m et de centre de gravité G, placé au voisinage de la Terre est soumis à une force attractive appelé son poids P. Le poids est un vecteur force, il possède donc 4 caractéristiques. G_T est le centre de gravité de la Terre (confondu avec son centre géométrique)

g est appelé intensité du champ de pesanteur terrestre. A la surface de la Terre g = 9,8 N/kg. Cela signifie qu’un objet de masse m = 1,0 kg posé à la surface de la Terre est soumis à une force d’intensité P = 9,8 N

Q5 : calculer le poids d’un objet de m = 50 kg posé sur Terre.

P = m.g = 50x9,8 = 4,9x10² N.

2. vecteur poids d’un corps sur la Lune

Sur la Lune l’intensité du champ de pesanteur lunaire g_Lune = 1,6 N.kg^-1. Sur la Lune 1 kg de matière est soumis à une force appelé son poids lunaire’ P_Lune = 1,6 N.

Sur la Lune le poids d’un corps est égal au produit de sa masse par l’intensité du champ de pesanteur lunaire :

P(Lune) = m.g_Lune

Q6 : donner les 4 caractéristiques du vecteur poids sur la Lune.

Réponse :

Q7 Comparer le poids de l’objet de masse m = 50 kg sur Terre et sur la Lune.

Q8 Cliquer sur l’animation suivante : différence entre masse et poids.

1) Pourquoi un corps retombe par terre quand on le lâche ?

2) Pourquoi la Lune ne tombe-t-elle pas sur Terre ?

3) Quelle sont les différences entre la masse et le poids ?

4. vecteur poids et vecteur force d’interaction gravitationnelle vidéo

Q9 Calculer la valeur de la force d’interaction gravitationnelle (ou force de gravitation) de la Terre sur l’objet de masse m = 50 kg (noté F_Terre_/objet). Le rayon de la Terre est R = 6,4x10³ km, m_Terre = 6,0x10²⁴ kg. Remplir le tableau suivant puis comparer le vecteur force d’interaction gravitationnelle qu'exerce la Terre sur un objet de masse m et le vecteur poids de ce même objet.

	Direction	Sens	Valeur
Poids		De G vers G_T
Force de gravitation	Vers le centre de la Terre	De G vers G_T
Conclusion	Identique	Identique	Identique

Le vecteur poids d’un objet est peu différent du vecteur force d’interaction gravitationnelle exercée par la Terre sur l’objet.

4. variation de l’intensité du champ de pesanteur g

D’une façon générale : Si z est l’altitude à laquelle se trouve l’objet et R_T le rayon de la Terre alors on a :

m.g = G.M_T.m/(R_T + z)²

Soit g = G.M_T./(R_T + z)²

On en déduit que g diminue quand l’altitude augmente.

Sur Terre, z = 0 on a :

g = G.M_T. /R_T²

A l’équateur : g = 9,79 N.kg^-1; Aux pôles : g = 9,83 N.kg^-1 : A Paris : g = 9,81 N.kg^-1

III. effet d’une force sur le mouvement d’un corps

1. Enoncé du principe d’inertie :

Q10 Clique sur l’animation suivante table à coussin d’air puis choisit mouvement sans frottement sur une table horizontale. Quelles sont les deux vecteurs forces agissant sur le solide ? Ces forces se compensent-t-elles ? Les représentez sur un schéma et donner leurs 4 caractéristiques. Choisir la chronophotographie de l’objet et de son centre d’inertie. Quel est le mouvement du centre d’inertie de l’objet ? 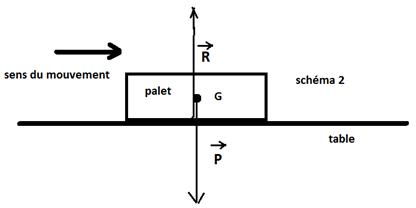Conclusion.

Un palet se déplace sur une table sans frottement. Son centre d'inertie à un mouvement rectiligne uniforme. Les 2 forces agissant sur lui sont son poids et la réaction du plan. Ses 2 forces se compensent:

Principe d’inertie : Dans un référentiel terrestre supposé galiléen, tout corps au repos ou possédant un centre d'inertie en mouvement rectiligne uniforme est soumis à des forces qui se compensent.

Un corps soumis à des forces qui se compensent et un corps qui n’est soumis à aucune force (cas d’un objet dans l’espace éloignés de toute masse) ont le même comportement.

Remarques : Ce principe est aussi vrai dans le référentiel géocentrique. Un principe résulte d’observations mais ne se démontre pas.

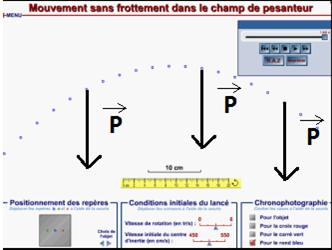
2. Forces exercées sur un projectile dans l’air :

Q11 Clique sur l’animation suivante table à coussin d’air puis choisit mouvement sans frottement dans un champ de pesanteur. Quel est le vecteur force agissant sur le solide ? La représenter sur un schéma et donner ses 4 caractéristiques. Choisir la chronophotographie de l’objet et de son centre d’inertie. Quel est le mouvement du centre d’inertie de l’objet ? Conclusion.

Un projectile est un corps lancé dans l’air au voisinage de la Terre. Dans l’air, un corps est soumis à son poids et à la force exercée par l’air sur le projectile. Si on néglige cette force de frottement alors le corps est en chute libre.

Le principe d’inertie permet de conclure que le mouvement du centre du projectile n’est pas rectiligne uniforme puisqu’il n’est soumis qu’à une seule force non compensée.

3. mouvement de la Lune autour de la Terre :

Q12 : cliquer sur le lien suivant mouvement des satellites et des planètes. Dans quel référentiel étudie–t-on le mouvement de la Lune ? Quel est le mouvement du centre d’inertie de la Lune dans ce référentiel ? Quel est la force s’exerçant sur ce la Lune ? Le mouvement de la Lune peut-il être rectiligne uniforme ? Pourquoi ?

Dans le référentiel géocentrique, la Lune possède un mouvement circulaire uniforme. D’après le principe d’inertie elle ne peut être soumise à des forces qui se compensent. Elle n’est soumise qu’à une seule force : la force d’interaction gravitationnelle de la Terre (et dans une moindre mesure aux forces d’interaction gravitationnelle des autres planètes du système solaire et du soleil).

Remarque : C’est parce qu’elle possède une vitesse suffisante que la Lune ne tombe pas sur Terre.

Animation : les phases de la Lune

Le système solaire
	U24-SP1	J’ai compris que la nature du mouvement observé dépend du référentiel choisi.
	U25	Je sais calculer la force d’attraction gravitationnelle qui s’exerce entre deux corps à répartition sphérique de masse.
	U26♥	Je sais que la pesanteur terrestre résulte de l’attraction terrestre.
	U27	Je sais comparer le poids d’un même corps sur la Terre et sur la Lune.
	U28♥SP4	Je sais qu’une force s’exerçant sur un corps modifie la valeur de sa vitesse et/ou la direction de son mouvement et que cette modification dépend de la masse du corps.
	U29-SP5	Je sais utiliser le principe d’inertie pour interpréter des mouvements simples en termes de forces.
	U30	Je sais mettre en oeuvre une démarche d’expérimentation utilisant des techniques d’enregistrement pour comprendre la nature des mouvements observés dans le système solaire.
	U31	Je sais analyser des documents scientifiques portant sur l’observation du système solaire.