Chapitre 2 : magnétostatique
Champ magnétique créé par un tronc de cône (ENAC 2000
Q1
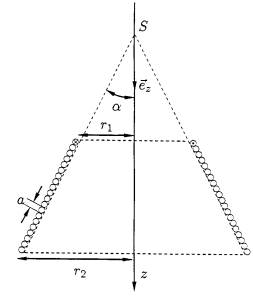
On réalise un bobinage en enroulant sur un tronc de cône,
jointivement suivant la génératrice, N
spires d'un fil de cuivre de diamètre a
et de résistivité ![]() . Le tronc de cône de sommet S, de demi‑angle au sommet
. Le tronc de cône de sommet S, de demi‑angle au sommet ![]() , est caractérisé par les rayons
, est caractérisé par les rayons ![]() et
et ![]() de ses deux bases. Chaque spire est repérée par sa
cote z qui mesure la distance qui
sépare son centre de S. On désigne
par
de ses deux bases. Chaque spire est repérée par sa
cote z qui mesure la distance qui
sépare son centre de S. On désigne
par ![]() le rayon de la spire située à la cote z.Exprimer le nombre N de spires qui constituent le bobinage
en fonction de
le rayon de la spire située à la cote z.Exprimer le nombre N de spires qui constituent le bobinage
en fonction de ![]() .
.

Q2
On désigne par dN le nombre de spires dont la cote est comprise entre z et z + dz. On considère que ces dN spires ont la même circonférence et qu'elles créent le même champ magnétique. Exprimer dN.

Q3
La résistance R d'un
fil de résistivité ![]() , de section
, de section ![]() et de longueur
et de longueur ![]() est donnée par la
relation :
est donnée par la
relation : ![]() . Calculer
R.
. Calculer
R.
![]()
Q4
Le bobinage est parcouru par un courant ![]() dans le sens
représenté sur la figure ci‑dessus. On désigne par
dans le sens
représenté sur la figure ci‑dessus. On désigne par ![]() la perméabilité du
vide. Calculer le champ magnétique
la perméabilité du
vide. Calculer le champ magnétique ![]() créé en S par une spire de rayon
créé en S par une spire de rayon ![]() .
.
![]()
Q5
En déduire le champ magnétique créé en S par la totalité du bobinage.
