Magnétostatique

Champ magnétique créé par un solénoïde (ENS Cachan 90)

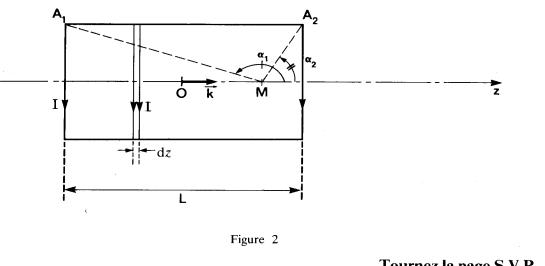
Soit un solénoïde de longueur L dont le nombre total de spires est N. Le rayon du solénoïde est R, il est placé dans l'air et on considère un point M de l'axe du solénoïde situé à une position  (figure 2) de centre O du solénoïde. Ce point M peut être caractérisé par les angles 1 et  2 définis à partir de l'axe O2 comme l'indique la figure 2.

  

Q1

Déterminer l'induction.  en M et exprimer la composante axiale de celle-ci en fonction de µo, N, I, L, 1 et  2 .

 

N.B.: On pourra se servir d e la valeur du champ magnétique créé par une spire en cherchant le champ élémentaire créé en M par un ensemble de spires circulaires contenues dans l'épaisseur dz et parcourues par le courant I.

Champ créé par une spire :

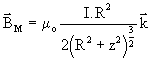
Q2

Application numérique: Calculer l'expression de l'induction  au centre si N = 300; L = 10 cm;               I = 0,5 A; R= 4 cm; µo = 4..10-7  unités SI