Un rayon lumineux monochromatique arrive sur une vitre d’épaisseur e = 7,00 mm en un point A avec un angle d’incidence i = 30,0°. L’indice de réfraction de la vitre pour ce rayon lumineux est n = 1,50. L’indice de réfraction de l’air est n (air) = 1,00. La célérité de la lumière dans le vide est c = 3,00x10⁸ m.s^-1. On veillera à respecter le nombre de chiffres significatifs.

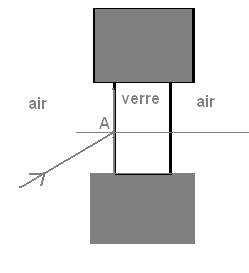1) Donner la définition de l’angle d’incidence ‘i’ et le dessiner sur le schéma.

2) Ecrire les 2 lois de Descartes sur la réfraction avec le nom des données de l’énoncé. L’angle de réfraction sera noté i₁.

3) Calculer l’angle de réfraction i₁ du rayon lumineux dans le verre et le représenter sur le schéma.

4) Calculer la célérité v de ce rayon dans le verre.

5) Le rayon réfracté arrive sur le dioptre verre air avec un angle d’incidence i₂. Donner sa valeur puis représenter le sur le schéma.

6) Calculer et représenter sur la figure l’angle de réfraction i₃ à la sortie de la vitre. Tracer le rayon émergent. Comparer sa direction avec celle du rayon incident arrivant au point A.

Corrigé

1) L’angle d’incidence est l’angle que fait le rayon incident avec la normale (perpendiculaire) au dioptre (surface de séparation entre le verre et l’air).

2) Les lois de Descartes :

Vidéo

- Première loi :

Le rayon réfracté et incident se trouve dans même plan.

- Deuxième loi :

n(air) sin i = n sin i₁

n(air)   indice de réfraction du milieu incident

n : indice de réfraction du milieu dans lequel se trouve le rayon réfracté

i : angle d’incidence

i₁ angle de réfraction

3) D’après la seconde loi de Descartes :

n(air).sin(i) = n.sin(i₂)

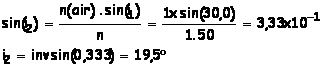
4)

Exercice similaire

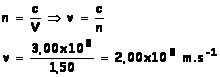
5) D’après le schéma ci dessus L’angle d’incidence sur le dioptre verre/air est égal à l’angle i₁ :

i₂ = i₁ = 19,5°

Exercice similaire.

6) D’après la seconde loi de Descartes :

n.sin i₂ = n(air).sin i₃

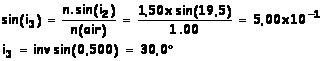
Le rayon émergent à la même direction que le rayon incident arrivant au point A. Globalement les rayons ne sont pas déviés par la vitre.