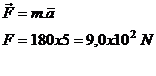HYDROLYSE BASIQUE DES ESTERS

1. Cinétique de la saponification du méthanoate d'éthyle

On étudie la cinétique de la réaction d'hydrolyse basique d'un ester, le méthanoate d'éthyle par la mesure de la conductance du mélange de méthanoate d'éthyle et de solution d'hydroxyde de sodium NaOH (ou soude) en fonction du temps.

Protocole expérimental :

On verse dans un becher une solution d'hydroxyde de sodium (ou soude) de concentration C₀ = 1,00.10 ^–2 mol . dm ^-3.On plonge la cellule conductimétrique dans la solution et on met en marche l'agitation. On mesure la conductance initiale G₀ à un instant que l'on désigne par t₀.On ajoute alors rapidement le méthanoate d'éthyle, en quantité égale à celle de la soude initiale. On mesure la conductance de la solution en fonction du temps. Les mesures sont reportées dans le tableau 1

Tableau 1 : Mesures des conductances et calculs de l'avancement en fonction du temps :

t (min)	0	3	6	9	12	15	45	Fin de réaction
G (mS)	?	2,16	1,97	1,84	1,75	1,68	1,20	1,05
Avancement x (mmol)	0	0,46	0,72	0,90		1,10	1,70	2,00

Données :

L'équation de la réaction étudiée est :

HCO₂ – CH₂ – CH₃ + HO^– = HCO₂^– + CH₃ – CH₂ – OH

À un instant t la conductance du mélange est donnée par la relation :

G_t = k×( × [Na⁺] + × [HO^–] + × [HCO₂^–] )

avec k la constante de cellule, k = = 0,0100 m et l la conductivité molaire ionique.

Les conductivités molaires ioniques de quelques ions à 25°C sont données dans le tableau ci-dessous :

ion	Na^+(aq)	HO^–(aq)	HCO2^–(aq)
en S.m².mol^-1	5,01.10 ^–3	19,9.10 ^–3	5,46.10 ^–3

Remarques :

Le volume de méthanoate d'éthyle est négligeable devant le volume V d'hydroxyde de sodium.Le volume du mélange est égal à 200 cm³ et la concentration C₀ = 1,00.10 ^–2 mol.dm ^-3. La solution d'hydroxyde de sodium étant nettement basique on négligera la présence des ions H₃O⁺ devant les autres ions du mélange réactionnel.

Questions :

Soient n₀ la quantité de matière initiale d'ions hydroxyde et d'ions sodium et n₀ la quantité de matière initiale de méthanoate d'éthyle.

1.1. On considère la solution d'hydroxyde de sodium de volume V à l'instant t₀.

1.1.1. Donner la concentration des ions dans cette solution à cet instant.

1.1.2. Montrer que la conductance G₀ peut s'écrire : G₀ =(k/V).n₀ . ( + ) (1)

1.1.3. En utilisant les unités conventionnelles du Système International, calculer la valeur de G₀.

1.2. On note x, l'avancement de la réaction à un instant t. Compléter le tableau d'avancement qui figure sur l'annexe 2 en indiquant les quantités de matière en fonction de x. L'annexe 2 est à rendre avec la copie.

1.3. On étudie la conductance de la solution en fonction du temps.

1.3.1. Montrer que la conductance du mélange à un instant t en fonction des quantités de matière initiales et de l'avancement x peut s'écrire :

G_t = (k/V).[ . n₀ + . (n₀ – x) + . x ] (2)

On veut montrer que la mesure de la conductance G_t permet de connaître l'avancement x en établissant une relation simple entre G_t et x.

1.3.2. Simplifier l'expression (2) pour montrer qu'on peut écrire G_t sous la forme G_t = a.x + b (3),
a et b étant des constantes qui contiennent les conductivités molaires ioniques et les quantités de matière initiales n₀.

1.3.3. À quelle grandeur correspond le coefficient b ? Quel est le signe de la constante a ?

1.3.4 Quelle serait l'allure de la représentation graphique G_t en fonction de x (relation (3)) ?

1.4. La relation (3) a permis de calculer les valeurs de l'avancement x qui sont indiquées dans le tableau 1 précédent.

1.4.1 Déterminer la valeur de l’avancement ‘x’ à t = 12 min

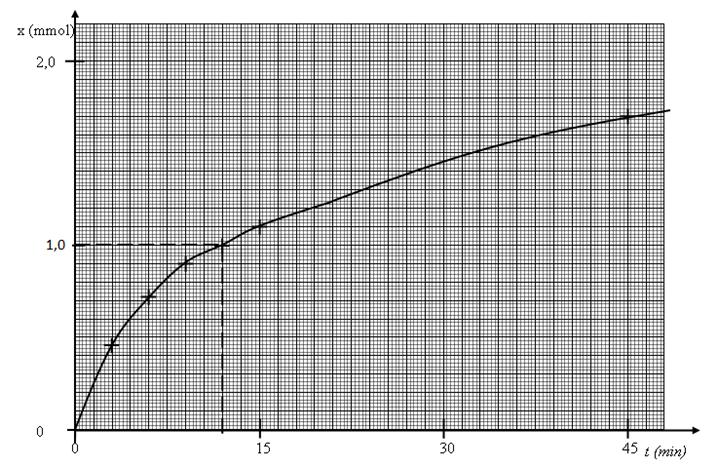
1.4.2 Tracer la courbe donnant les variations de x en fonction du temps.

On prendra comme échelle en abscisse 1 cm pour 3 min et en ordonnée 1 cm pour 0,20 mmol.

ANNEXE 2 à rendre avec la copie

Tableau 2 : Tableau d'avancement

équation chimique		H–CO2–CH2–CH3 + HO^– = HCO2^– + CH3–CH2–OH
État du système	Avancement (mol)	Quantités de matière (mol)
État initial	0	n0	n0	0	0
État intermédiaire	x

Hydrolyse basique des esters (2004/09 Antilles)

1.1.1. H–CO₂–CH₂–CH₃ + HO^– = HCO₂^– + CH₃–CH₂–OH

A t = 0 seul les ions N_a⁺ et HO^- sont présents dans la solution.

La réaction de dissolution de la soude dans la solution est :

NaOH_(s) = Na⁺_(aq) + HO^–_(aq) transformation totale

[HO^–_(aq)] = [Na⁺_(aq)] = C₀ = 1,00.10^–2 mol.L^-1 (1dm³ = 1L)

1.1.2.

G₀ = k×( ×[Na⁺_(aq)] + ×[HO^–_(aq)]) = k×C₀×( + )

G₀ = n₀ ( + )

1.1.3. Calcul de G_o

G₀ = k×C₀×( + )

Attention les concentrations sont dans l’unité légale : C₀ en mol.m^–3,

1 mol.L^-1 = 1 mol/(10^-3 m³)

Co = 1,00.10^–2 mol/L = 1,00.10^–2 /( 10^-3 m³) = 1,00x10¹ mol.m^-3

G₀ = 0,0100×1,00.10¹ ´(5,01.10^–3 + 19,9.10^–3)

G₀ = 0,0100×1,00.10^–2 ´(5,01+19,9) = 2,49 mS

1.2. équation chimique		H–CO2–CH2–CH3 + HO^– = HCO2^– + CH3–CH2–OH
État du système	Avancement (mol)	Quantités de matière (mol)
État initial	0	n0	n0	0	0
État intermédiaire	x	n0 – x	n0 – x	x	x

1.3.1. La conductance de la solution à l’instant t est :

G_t = k ×( ×[Na⁺_(aq)] + ×[HO^–_(aq)] + ×[HCO₂^-_(aq)] )

G_t = k ×( ×+ ×+ ×)

G_t= ×( ×n₀ + ×(n₀ – x) + ´ x)

1.3.2. G_t= ×( ×n₀ + ×(n₀ – x) + ´ x)

G_t = × × n₀ + × × n₀ – × ´ x + ´ x

G_t= .x ( – ) +×n₀ ( + )

G_t = ax + b

a = ×( – )

b = ×n₀ ( + )

1.3.3.

G₀ = k×C₀×( + )

b = ×n₀ ( + )

b = G₀

ion	Na^+(aq)	HO^–(aq)	HCO2^–(aq)
en S.m².mol^-1	5,01.10 ^–3	19,9.10 ^–3	5,46.10 ^–3

>

a = –

donc a < 0

1.3.4. G_t = a.x + b

La représentation de G_t en fonction de x serait une droite de pente négative et qui ne passe pas par l’origine ( pour x = 0 , G₀ = b ).

1.4.1. Calcul de x à t = 12 min, G = 1,75 mS

G_t= .x ( – ) +×n₀ ( + )

G_t - ×n₀ ( + ) = .x ( – )

[G_t.V/k - n₀ ( + )] /( – ) = x

A.N.

x = 1,00x10^-3 mol

1.4.2. Avancement x de la réaction de saponification du méthanoate d'éthyle en fonction du temps.

RECORD DE SAUT EN LONGUEUR À MOTO (Polynésie 09/2009)

La phase d’accélération du motard.

1. échelle1 cm (document) Û 2 m (réel)

G₁G₃ = 6,4 cm sur le document donc G₁G₃ (réel) = 6,4 × 2 / 1 = 12,8 m

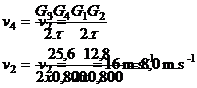
G₃G₅ = 12,8 cm sur le document donc G₃G₅ (réel) = 12,8 × 2 / 1 = 25,6 m

2. Échelle des vitesses : 1 cm Û 2 m.s^-1 donc les longueurs des vecteurs viteses sont :

L() = 8,0 × 1/2 = 4,0 cm

L() = 16,0 × 1/2 = 8,0 cm

Rappel : Les vecteurs vitesses sont tangents à la trajectoire et orientés dans le sens du mouvement.

3. = –

Le vecteur variation de vitesse démarre du point G₃.

4. Vecteur accélération au point G₃ :

.

1 cm Û 2 m.s^-1 ;

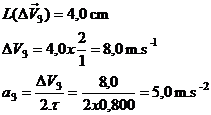
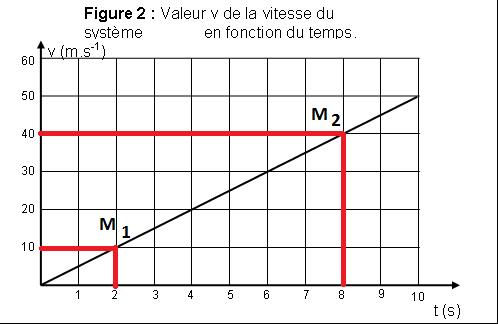
5.1. la vitesse est proportionnelle au temps  car Le graphe de la figure 2 est une droite qui passe par l’origine,

v = k.t avec k pente de la courbe

L’accélération a est défini par :

a =  ;

a = = k

L’accélération de la moto est constante.

5.2. Pour déterminer l’accélération il faut calculer la pente de la courbe v = f(t) . On prend 2 points de la droite :

entre les points

M₁ (t₁ = 2 s ; V₁ = 10 m.s^-1)

M₂ ( t₂ = 8 s ; V₂ = 40 m.s^’1)

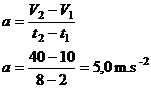
On retrouve bien la valeur obtenue graphiquement en 4.

5.3. v = 160 km/h = 160x1000/3600

v = 44,4 m.s^-1

v = a.t

t = v/a = 44,4/5,0

t = 8,9 s

A t = 8,9 s la moto attaint la vitesse de 44,4 m.s^-1

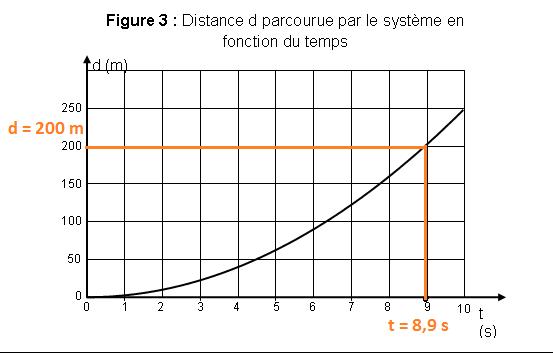
Graphiquement avec d = f(t) on trouve la distance parcourue par la moto quand elle atteint la vitesse v = 160 km/h

d = 200 m

6.1 vidéo

Lorsqu'un système matériel A exerce une force sur un système matériel B, alors celui-ci exerce sur le système matériel A une force opposée :

Les droites d'actions des 2 forces sont confondues.

6.2 D’après le principe d’interaction la force exercée par la moto sur la route est opposée à la force exercée par la route sur la moto :

6.3 c) Pour faire l'étude mécanique du système, il faut toujours définir dans l'ordre:

1) Le système: (moto, motard)

2) Le référentiel : la terre supposée référentiel galiléen, dans lequel on pourra appliquer la seconde loi de Newton. 

3) Le repère lié au référentiel :

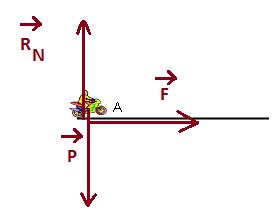
4) Somme des forces extérieures au système :

Les vecteurs poids et réaction normale au poids sont opposés.

6.4 Tracé des vecteurs forces :

6.5