Chapitre 7 : circuit RL

Résistance d’une bobine réelle (Polynésie 2006 6 points )

Dans tout l’exercice, on tiendra compte de la précision des données afin d’exprimer les résultats numériques en accord avec cette précision.

Un étudiant, curieux, veut vérifier la valeur de la résistance r d’une bobine réelle d’inductance
250 mH, modélisée sous forme d’un dipôle (r , L) en série. La tension en fonction du temps dans le cas général d’un courant électrique d'intensité i(t) aux bornes d’une telle bobine est donnée par la relation :

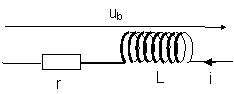
u_b = r.i + L.

Il dispose de tout le matériel souhaitable et procède à plusieurs essais.

A – En régime permanent

Pour mesurer la valeur de r, l’étudiant réalise un circuit comportant un générateur de tension continue de valeur E = 6,0 V de résistance interne négligeable, un ampèremètre numérique, un voltmètre numérique, des fils de connexion et la bobine à étudier.

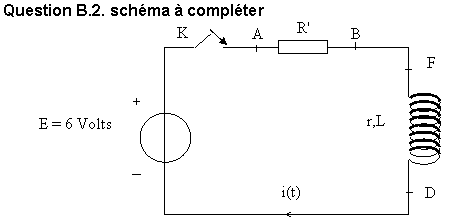
1. Compléter le schéma du circuit en indiquant les positions de l’ampèremètre et du voltmètre (annexe à rendre avec la copie). Faire figurer la tension U_g = E (tension aux bornes du générateur) ainsi que la tension U_b= (tension aux bornes de la bobine). On négligera la tension aux bornes de l’ampèremètre.

2. Les mesures des appareils donnent U_b = 5,95 V et I_b = 410 mA. En déduire la valeur r₁ de la résistance de la bobine dans ce cas particulier. Justifiez votre démarche.

B – En régime transitoire

L’étudiant modifie le montage précédent auquel il ajoute une résistance R’ = 10,0 W en série.

Il remplace les appareils de mesure par un système d’acquisition informatisé qui lui donne les variations de i(t) obtenues à la fermeture de l’interrupteur. La tension du générateur reste fixe et égale à 6,00 V.

1. Quel est alors le phénomène observé dans le circuit ?

2. Sur le schéma du circuit modifié (annexe à rendre avec la copie), indiquer comment brancher le système d’acquisition (voie d’entrée et voie de référence) afin d’obtenir une
tension proportionnelle à l’intensité du courant dans le circuit. Justifier votre réponse.

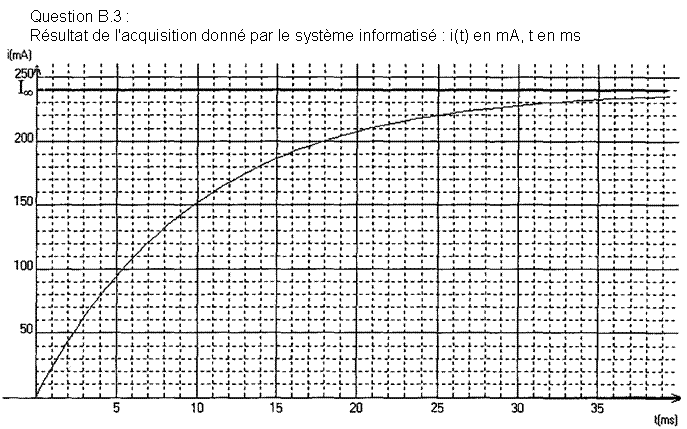
3. Déterminer la valeur de la constante de temps t à partir du document obtenu par le système d’acquisition. Détailler clairement la méthode utilisée sur le graphe donné en annexe à rendre avec la copie.

4. 4.1. La valeur de t de ce circuit est égale au rapport où R représente la résistance électrique totale du circuit. Donner l’expression littérale de t en fonction des paramètres du circuit et vérifier par une analyse dimensionnelle que t est homogène à un temps.

4.2. La bobine ayant une inductance L = 250 mH, déduire la valeur r₂ de sa résistance.

5. On considère que l’intensité i(t) atteint la valeur limite I_¥ = 240 mA au bout d’une durée
5 fois supérieure à t.

5.1. Quel est alors le régime de fonctionnement de la bobine ?

5.2. Exprimer r, résistance de la bobine en fonction de E, I_¥ et R’. Calculer sa valeur r₃.

6. Les trois valeurs r obtenues dans les parties A et B sont-elles cohérentes entre elles ?

C – En régime oscillatoire

Cette bobine est branchée aux bornes d’un condensateur de capacité C = 4 mF,
préalablement chargé par un circuit annexe non représenté, selon le schéma ci-dessous :

1. 1.1. Rappeler l’expression littérale de la période propre T₀ d’un oscillateur LC.

1.2. Calculer la valeur de cette période T₀.

2. 2.1. On branche un oscilloscope aux bornes du condensateur et on observe sur l’écran
des oscillations pseudo-périodiques de pseudo-période T.

Interpréter l’amortissement des oscillations.

2.2. On constate, avec une base de temps de 2 millisecondes par division,
que 2 pseudo-périodes occupent entre 6,2 et 6,4 divisions.

Donner un encadrement de la pseudo-période T ainsi mesurée.

2.3. Comparer ce résultat à T₀.

ANNEXE à rendre avec la copie