Modélisation d'une alarme ( Métropole 2005 ;
4 points)
Un élève,
dans le cadre de travaux personnels, souhaite étudier un système d'alarme.
Après avoir modélisé la mise sous tension du circuit de commande de la sirène (première partie de l'exercice), il cherche à savoir si des phénomènes inductifs peuvent provoquer le déclenchement intempestif de la sirène (deuxième partie de l'exercice).
I.
Première partie :
fonctionnement simplifié d'une alarme d'appartement
Après
avoir mis sous tension l'alarme d'un appartement, il faut pouvoir disposer
d'une durée suffisante pour
sortir sans la déclencher. Pour cela certains dispositifs utilisent la charge
et la décharge d'un
condensateur.
Le circuit
est alimenté par une batterie d'accumulateurs de force électromotrice (f.e.m.)
E.
Le schéma
simplifié de l'alarme est le suivant.
E B
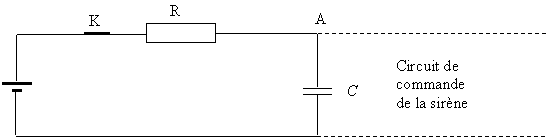
Schéma
1
R = 47 kW; C= 1,1 ´ 103 µF; E = 9,0 V
La mise
sous tension de l'alarme correspond à la fermeture de l'interrupteur K.
Le circuit de commande de la sirène est tel
qu'à la fermeture de la porte de l'appartement, le condensateur est mis en
court-circuit (ses
armatures sont alors reliées par un fil conducteur non représenté sur le
schéma).
1. Étude de la charge du condensateur dans le circuit RC
Pour
étudier la charge du condensateur de capacité C, l'élève visualise la tension uAB = f(t) à ses bornes à l'aide d'une interface reliée
à un ordinateur. Le circuit de commande de la sirène n'est pas relié au condensateur lors de cette
expérience.
L'acquisition
commence lors de la fermeture de l'interrupteur (K), le condensateur étant préalablement déchargé.
L'élève obtient la courbe uAB
= f(t) représentée EN
ANNEXE À RENDRE AVEC
1.1. Indiquer
sur
L'entrée et la masse de l'interface sont respectivement équivalents à une voie Y et à la masse d'un oscilloscope.
1.2. En
utilisant une méthode au choix, déterminer, à partir
de la courbe uAB =
f(t) (Figure 2 DE L'ANNEXE À
RENDRE AVEC
1.3. Donner l'expression de la constante de temps t en fonction des caractéristiques du circuit et
vérifier par le calcul la valeur trouvée à la question 1.2.
2.
Déclenchement de l'alarme
Ce circuit
commande une sirène (voir Schéma 1) qui se déclenche dès que la tension aux bornes du condensateur
atteint la valeur de 8 V.
2.1. À l'aide
de la courbe uAB =
f(t) donnée Figure 2 DE L'ANNEXE À RENDRE AVEC
en indiquant clairement cette durée sur le
graphe.
2.2.
Expliquer pourquoi le fait de fermer la porte empêche l'alarme de se
déclencher.
II.
Deuxième partie:
l'alarme peut-elle se déclencher de manière intempestive ?
Des phénomènes inductifs peuvent apparaître dans le circuit.
Celui-ci est alors analogue à un circuit RLC série.
Pour comprendre l'influence de l'inductance l’élève réalise, au laboratoire,
le montage ci-contre, avec les composants dont les caractéristiques sont
données au schéma 2.
L'élève enregistre comme dans la première
partie de l' exercice la tension uAB
= f(t) aux bornes du condensateur, pour deux valeurs de résistance R1
= 160 W et R2 = 2,4 kW . Il obtient les courbes a et
b ci-dessous.
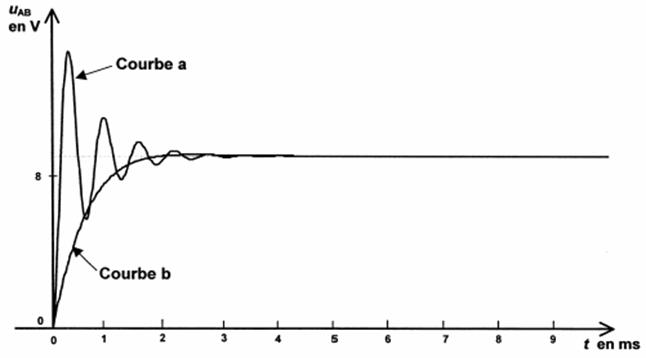
1. Donner les
noms des régimes associés aux courbes a et b. Indiquer pour chacun d'eux la
valeur donnée à la résistance R,
en précisant la raison de ce choix.
Pour
étudier les régimes de charge du condensateur, on appliquera les mêmes
conclusions que dans le cas de la décharge du condensateur en série avec une
bobine et une résistance.
2. À partir
de ces courbes, montrer que l'intensité du courant dans le circuit s'annule au
bout d'une
durée suffisamment longue.
3. En
appliquant la loi des tensions, trouver la valeur finale de la tension uAB.
4. Quel inconvénient présenterait le régime associé à la courbe (a) si cette modélisation correspondait au circuit de déclenchement de l'alarme précédente ?
5. Dans un
circuit de capacité C, d'inductance L et de résistance R, on évite les
oscillations si la condition suivante est vérifiée: 
³ 1. La valeur de l'inductance dans le circuit d'alarme est
supposée inférieure à 1 mH.
Dire, en
justifiant la réponse, si des oscillations peuvent apparaître dans le circuit
d'alarme étudié dans la première
partie, immédiatement après la fermeture de l'interrupteur K.
ANNEXE
Figure
1
E
