Sonde thermique (bac Antilles 2005 )

corrigé

On peut constituer une sonde thermique à l’aide d’un dipôle (R,C) série. On réalise le circuit suivant :

Le condensateur a une capacité C = 1,0 mF. Le conducteur ohmique est une thermistance : la valeur R de sa résistance dépend de la température. On le place dans une enceinte dont la température interne est notée q. Un système d’acquisition permet d’enregistrer l’évolution au cours du temps de la tension u_C aux bornes du condensateur. Aide mathématique :

0,63 × 4,0 = 2,5

0,37 × 4,0 = 1,5

e^0 = 1

Étalonnage de la sonde

Protocole expérimental :On souhaite tracer la courbe de l’évolution de la valeur de la résistance de la thermistance en fonction de la température. On réalise le protocole suivant :Le condensateur est initialement déchargé et les interrupteurs K 1 et K 2 sont ouverts. À t = 0, on ferme K 1 et on enregistre l’évolution de la tension u_C jusqu’à la fin de la charge du condensateur. Ensuite, on ouvre K 1 et on ferme K 2 : le condensateur se décharge complètement. On ouvre enfin K 2. On modifie la température de l’enceinte et on recommence le protocole précédent. On opère pour plusieurs valeurs de température et on obtient le graphique suivant :

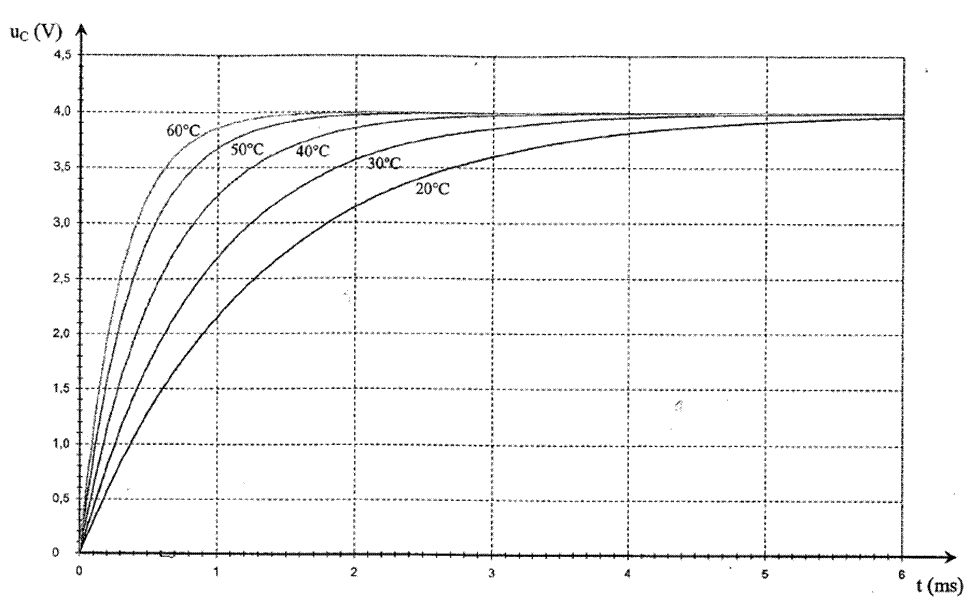
Q1

a) À l’aide des résultats expérimentaux, étudions la charge du condensateur. Établir la relation entre la tension E aux bornes du générateur, la tension u_R aux bornes du conducteur ohmique et la tension u_C aux bornes du condensateur.

b) Déterminer l’équation différentielle vérifiée par la tension u_C pendant la phase de charge.

Q2

a) La solution analytique de cette équation est de la forme : u_c =A + B.exp(-t/RC). En tenant compte des conditions finales de la charge, déterminer A.

b) En tenant compte des conditions initiales de la charge, déterminer B.

c) Déduire l’expression de u_C.

Q3

a) On donne l’expression de la constante de temps du dipôle (R, C) : t = RC. Vérifier par analyse dimensionnelle l’homogénéité de cette formule.

b) Déterminer la valeur t₁ de la constante de temps, relative à la température q₁ = 20°C, à partir du graphique. Expliquer la méthode employée.

c) En déduire la valeur R 1 de la résistance correspondante. Procéder de la même manière pour les autres températures et compléter le tableau de l’annexe à rendre avec la copie.

Q4

2. Mesure d’une température :

a) Tracer sur papier millimétré (à rendre avec la copie) la courbe d’étalonnage R = f( q) en respectant l’échelle suivante : abscisse : 1 cm pour 5°C ordonnée : 1 cm pour 0,1 kW

b) Essayons la sonde thermique en la plaçant dans une enceinte de température interne q à déterminer. On mesure la résistance de la thermistance à l’aide d’un ohmmètre et on obtient : R = 0,50 kW. En vous servant de la courbe d’étalonnage, déterminer la température de l’enceinte.

ANNEXE 2 (À RENDRE AVEC LA COPIE)

(Seules les case blanches sont à compléter)

Température q (°C)	q1 = 20	25	30	35	40	45	50	55	60
Constante de temps t (ms)	t1 =
Résistance R (kW)	R1 =	1,07		0,74		0,49		0,34