Chapitre 14 : oscillateur mécanique horizontal, système solide ressort

Oscillateur mécanique

corrigé

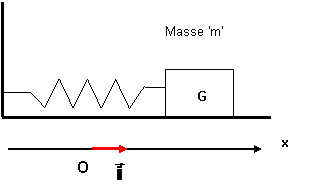
Une table à digitaliser est un dispositif permettant d'enregistrer les positions d'un système mécanique en fonction du temps. Un solide S, de masse m = 100 g est accroché à un ressort à spires non jointives. On enregistre la position de son centre d'inertie G au cours du temps à l'aide de l'ordinateur connecté à une table à digitaliser horizontale. L'oscillateur décrit ci-dessus est équivalent à un solide de masse m accroché à un seul ressort à spire non jointive de constante de raideur k. La position du centre d'inertie G du solide est repéré par son abscisse x dans le repère. À l'équilibre le centre d'inertie G coïncide avec l'origine O du repère. On réalise 3 enregistrements dans les conditions suivantes :

a) soufflerie à puissance maximale ; b) puissance de la soufflerie légèrement diminuée ; c) puissance de la soufflerie fortement diminuée. On obtient les enregistrements 1,2, 3 ci-dessous.

Q1

a) Indiquer pour chacun des trois enregistrements :

- la condition (a, b ou c) de fonctionnement de la soufflerie ;

-le régime d'évolution (périodique, pseudo périodique apériodique ). Dans toute la suite on se place dans le cas où les frottements sont négligeables.

b) Sur un schéma, représenter les forces s'exerçant à l'instant t sur le solide S et les nommer.

Q2

a) En appliquant la deuxième loi de Newton, montrer que l'équation différentielle du centre d'inertie G du solide S est :

b) La solution analytique de l'équation différentielle est de la forme :

Comment se nomment les constantes Xm et f_o ? Déterminer leur valeur sachant que S est lâché à t = 0 sans vitesse initiale au point d'abscisse x = 10,0 cm.

Q3

a) Déterminer la période propre To de l'oscillateur en utilisant l’un des enregistrements précédents.

b) A l'aide d'une analyse dimensionnelle, déterminer l'expression de la période propre To parmi celles proposées ci-dessous :

c) En déduire la valeur numérique de la constante de raideur k du ressort équivalent.

Q4

a) Déterminer l’expression littérale puis numérique de la coordonnée de la vitesse v_x du centre d’inertie du solide. Dessiner l’allure de la courbe v_x = f(t).

b) Même question pour l’accélération a_x du centre d’inertie du solide.

c) On considère l’intervalle de temps 0 < t < To . A quel instant (à exprimer en fonction de To) la norme ‘v’ de la vitesse est-elle maximale? Pourquoi ?

d) Même question pour la norme minimale de la vitesse.

Q5 Etude statique

On dispose le ressort verticalement.

a) Déterminer l’allongement x, du ressort de raideur k, au bout duquel on suspend une masse m = 50 g. On effectuera l’étude mécanique et on prendra g = 9,8 N.kg^-1.

b) Donner une méthode ‘statique’ permettant de déterminer la raideur k du ressort.