I) Les lois de Kepler loi n°1 ou loi des orbites elliptiques 1605 Toutes les orbites des planètes sont des ellipses dont le soleil occupe l'un des foyers. loi n°2 ou loi des aires (1604) Pendant des intervalles de temps égaux Dt la planète balaye des surfaces 'S' de l'ellipse égales. Schéma:     Si  Dt = t1-t0 = t3-t2 alors S1 = S2 loi 3 ou loi des périodes La période de révolution au carré divisée par le demi-grand axe 'a' au cube est une constante. Elle ne dépend pas de la planète mais uniquement de la masse MS du Soleil et de la constante d'attraction universelle G : G = 6,67.10-11N.kg-2.m2 ;MS = 1,96.1030 kg. II) La loi de gravitation de Newton 1) force d'attraction gravitationnelle  Un corps ponctuel A de masse mA exerce sur un corps ponctuel B de masse mB une force d'attraction gravitationnelle telle que : : vecteur unitaire (norme sans unité, et égale à 1, de direction la droite AB et de sens de A vers B. FA/B exprimé en Newton (N).   L'expression de cette force d'attraction gravitationnelle s'applique également pour des objets à symétrie sphérique,  pour lesquelles la matière est répartie uniformément dans toutes les directions. La force gravitationnelle s'applique alors au centre d'inertie du solide. III) Le mouvement circulaire uniforme 1) la base de Frénet Dans le cas des mouvements circulaires on n'utilise pas  le repère cartésien, mais le repère de Frénet, défini par deux vecteurs orthonormés dans le plan : Soit un point P mobile décrivant une trajectoire curviligne la base de Frénet à l'instant t est : :  vecteur unitaire tangent à la trajectoire au point P, orienté généralement dans le sens du mouvement. :  vecteur unitaire, normal à la trajectoire, et centripète. 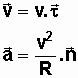2) Vecteur accélération pour un mouvement circulaire uniforme Pour un mouvement circulaire uniforme de rayon de trajectoire R, le vecteur accélération et le vecteur vitesse d'un point mobile sont : L'accélération est centripète ( orientée vers le centre de la trajectoire).

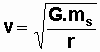
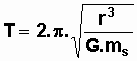
3) Vitesse et accélération du centre d'inertie d'une planète, dans le cas d'un mouvement circulaire uniforme Dans le cas d'un mouvement circulaire uniforme les vecteur vitesse et accélération du centre d'inertie sont: avec: Dans le cas particulier du mouvement circulaire uniforme, la période de révolution de la planète autour du soleil est :  IV) Satellites de la terre en mouvement circulaire uniforme 1) Cas d'un satellite quelconque Le mouvement des satellites se fait dans un plan contenant le centre d'inertie de la terre GT. En effet la force de gravitation exercée par la terre sur le satellite est centripète.  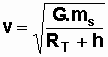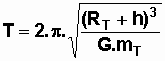Schéma : La vitesse et la période d'un satellite décrivant une orbite circulaire centrée sur le centre d'inertie de la Terre, sont : h: altitude du satellite(m); RT = 6400 km rayon de la terre. mT =6.1024kg , masse de la terre. G = 6,67.10-11N.kg-2.m2 constante de gravitation universelle. 2) Satellite géostationaire Un satellite est géostationnaire s'il est toujours situé au-dessus du même point de la terre. Il est immobile dans un référentiel terrestre. Comme son plan orbital doit contenir le centre de la terre, son orbite est dans le plan de l'équateur. Sa période de révolution T est égale à la période de rotation de la terre dans le référentiel géocentrique. Cette période est appelée également jour sidéral. T =23 h 56 min 4 s = 86164 s 3) Corps en impesanteur Considérons un satellite en orbite autour de la terre !  Dans le référentiel satellite, la somme des forces extérieures appliquée à un objet est nulle. Celui ci 'flotte' dans cette merveille de technologie.  On dit que le solide est en impesanteur.  Remarque: dans le référentiel satellite, le poids de l'objet appelé poids apparent est nul.