I) Force de rappel exercée par un ressort 1) Définition Soit un ressort de longueur à vide lo. On modifie sa longueur en exerçant une force de tension à son extrémité libre, en le comprimant ou l'étirant. La nouvelle longueur du ressort est notée 'l'. L'allongement 'a' du ressort est alors: a = l-lo. Quand on comprime ou étire un ressort, celui ci exerce alors une force de rappel proportionnelle à son allongement.  Le coefficient de proportionnalité est appelé la raideur 'k' du ressort. En orientant l'axe dans le sens de l'élongation du ressort l'expression vectorielle de la force de rappel est: F, valeur de la force de rappel en Newton (N); l , longueur et lo, longueur au repos, du ressort en mètre (m); : vecteur unitaire orienté dans le sens de l'élongation k : raideur du ressort (N.m-1) 2 ) Expression de la force de rappel en fonction de l'abscisse de l'extrémité du ressort  Si on choisit comme origine des axes l'extrémité libre du ressort au repos (longueur lo), alors l'allongement du ressort est :  x = l - lo . L'allongement est égal à l'abscisse 'x' de l'extrémité libre du ressort.  Schéma: Que le ressort soit comprimé ou étiré la relation précédente est la même ! II) Oscillation libre non amortie  1) Etude mécanique On considère un solide de masse 'm' relié à un ressort dont l'autre extrémité est fixe :  Schéma: L'origine O du repère est placée au point Go position du centre d'inertie de la masse quand le ressort est au repos. Par conséquent l'abscisse 'x' du point G quand le ressort à un longueur l est : x = l-lo. Somme des forces extérieures appliquées à la masse 'm': Le plan est sans frottement donc la réaction est normale au plan. Elle compense le poids par conséquent : 2) Equation différentielle du mouvement La seconde loi de Newton ou principe fondamental de la dynamique dit que la somme des forces extérieures agissant sur le solide est égale au produit de la masse 'm' du solide par l'accélération de son centre d'inertie G (d'abscisse 'x'). Par conséquent l'équation différentielle du mouvement d'un solide de masse 'm' , soumis à une force de rappel d'un ressort de raideur k, sur un plan horizontal sans frottement est :

3) Solution de l'équation différentielle On démontre que la solution de cette équation différentielle est de la forme : Avec :To(s), période propre de l'oscillateur (s); Xm(m), amplitude des oscillations ; f(rad), phase à l'origine des dates. Le solide est le siège d'oscillations mécaniques libres sinusoïdales. La période propre To d'un oscillateur élastique en translation est : m : masse du solide (kg) ;k : raideur du ressort (N/m). Remarque : pour de petites oscillations la période propre d'oscilllation ne dépend pas de l'amplitude. III) Oscillation libre amortie On distingue 2 régimes d'oscillations suivant l'importance des frottements : Le régime pseudo périodique, et le régime apériodique. 1) Régime apériodique Le plan sur lequel se déplace le solide relié au ressort, exerce une force de frottement. On étire le ressort d'une longueur x = l-lo.  Lorsque les frottements sont très importants le système mécanique {ressort, solide} revient sans osciller à sa position initiale. Ce régime est appelé régime apériodique.   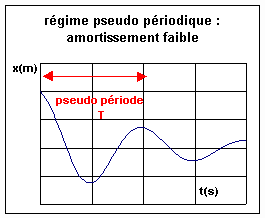2) Régime pseudo-périodique Lorsque les frottements sont faibles, le système mécanique est le siège d'oscillations amorties d'allure sinusoïdale.  Le phénomène ne se répète pas identique à lui-même, on parle de phénomène pseudo périodique. La pseudo période T est peu différente de la période propre d'oscillation libre non amortie ( en faite elle est légèrement supérieure).      IV) Le phénomène de résonance Lorsqu'un excitateur impose des oscillations forcées à un oscillateur, celui ci entre en résonance pour une période T proche de sa période propre To. Son amplitude xm est alors maximum. Ce phénomène est appelé la  résonance. Si T (excitateur)» To alors xm= xm(max). Schéma: