Chapitre 6 : charge et décharge d'un condensateur : dipôle RC
|
I) Les condensateurs 1) Composition Un condensateur est constitué de 2 armatures séparées par un isolant. La tension uab aux bornes du condensateur est égale à la charge électrique qa portée par l'armature 'a' divisée par la capacité C du condensateur:
Unités : C en farads(F); qa en coulomb (C); uab en volt (V); i en ampère(A).
2) Principe de fonctionnement Le générateur peut être considéré comme une pompe à électrons. À chaque fois qu'un électron arrive sur l'armature A un électron de l'armature B se dirige vers la borne positive de la pile (puisque le courant est le même en tout point d'un circuit série). Si une charge négative quitte l'armature A, alors il apparaît sur cette armature une charge positive (les électrons ne se déplaçant pas entre les armatures à cause de l'isolant). À chaque instant la charge qa=-qb. Petit à petit il se crée une différence de potentiel électrique entre les armatures A et B. Quand cette différence de potentiel est égale à celle de la pile le condensateur est chargé. Le courant ne circule plus dans le circuit. II) Réponse du dipôle RC à un échelon de tension 1) Etude expérimentale
Avant l’instant t = 0 l'interrupteur est en position 2 le condensateur est déchargé. Puis à t = 0 on bascule l'interrupteur en position 1, le condensateur se charge. 2) Expression mathématique de u(t) Dans un circuit série RC soumis à un échelon de tension E la loi des mailles donne : E = R.i + uc E = RC (duc/dt) + uc La solution de cette équation différentielle en uc est: uc = A + B.e-t/t Les conditions initiales et la validité de l'expression quelque soit l'instant 't' permettent de déterminer les constantes A et B et t . Par conséquent : uc = E (1-e-t/t ) avec t = R.C 3) Constante de temps t du circuit RC Par définition la constante de temps t du circuit RC série est égale au produit de la résistance R par la capacité C du condensateur. t = R.C Unité : la seconde(s). |
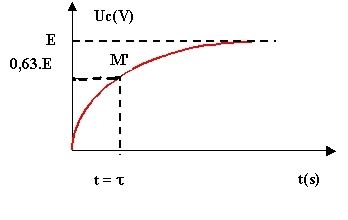
Au cours de la charge du condensateur à travers une résistance R, sous une tension E du générateur : A t = t, uc = 0,63.E A t = 5.t , uc = 0,99.E (le condensateur est pratiquement chargé) Pour déterminer graphiquement t on trace la tangente à la courbe uc(t) en t = O. Cette tangente coupe l'asymptote u = E en un point M d'abscisse t = t .
On peut également prendre
le point M' de la courbe uc(t) d'ordonnée 0,63 x u(max) = 0,63 x E et d'abscisse t = t .
III) Décharge d'un condensateur dans la résistance 1) Etude expérimentale Le condensateur étant chargé, on bascule l'interrupteur en position 2. 2) Expression mathématique de u(t) Au cours de la décharge du condensateur la loi des mailles donne: uc+Ri = 0 donc uc+RC.(duc/dt) = 0 La solution de cette équation différentielle en uc est de la forme: uc = A.e-t/t Les conditions initiales et la validité de cette solution quelque soit l'instant 't' nous donne la solution: uc = E.e-t/t *à t = t, uc = 0,37.u(max) = 0,37.E *pour déterminer
graphiquement t
tracer la
tangente à la courbe à t = 0s. Cette droite coupe l'axe des abscisses
en IV) Energie électrique Ee emmagasinée par un condensateur 1) Définition L'énergie électrique Ee emmagasinée par un condensateur de capacité C possédant une tension u à ses bornes et une charge q sur une des armatures est :
Unité: C en farad(F), u en volt(V), q en coulomb (C), Ee en joule (J). 2) Continuité de la tension aux bornes du condensateur L'énergie du condensateur ne peut varier brusquement. Par conséquent la tension aux bornes d'un condensateur est continue au cours du temps. Il en va de même pour la charge q car q=C.u Par contre l'intensité du courant i=dq/dt. présente une discontinuité à la charge ou à la décharge. |