1) Définition
Une bobine ou solénoïde est constituée d’un enroulement de fil conducteur posé sur un support isolant.
2) Expression générale de la tension aux bornes d’une bobine
Soit une bobine de résistance ‘r’ et d’inductance L, lorsqu’elle est parcourue par un courant d’intensité i quelconque la tension à ses bornes est :
unité : U en volt(V) ; i en ampère(A) ; r en ohm(W ) ; L en Henry(H) ;
II) Etablissement du courant dans une bobine
1) Expression théorique
On considère un
circuit comportant en série:
*un générateur
parfait de f.e.m E et un interrupteur.
*une bobine d'inductance
L de résistance interne r
*un conducteur ohmique
de résistance R
A l'instant t = 0 on ferme l'interrupteur.

La loi des mailles donne:
E = R.i + Ldi/dt + r.i
La solution de cette équation différentielle en i est de la forme :
i = A.(1-Bek.t)
La condition initiale (i = 0) et la validité de cette expression quel que soit l'instant ‘t’ donne la solution suivante :
t est la constante de temps d’établissement du courant dans le circuit.
Unité : i (A) ; E échelon de tension (V); r,R (W ); L(H); t (s).
3) Détermination graphique de la constante de temps t
Pour déterminer
graphiquement t ,
il suffit de tracer la tangente à la courbe à t = 0, celle
ci coupe l’asymptote horizontale i = i(max) en un point M d’abscisse t
= t.
Remarque :
A t = t l’intensité i(t ) = 0,63.i(max)
à t = 5.t , i(5.t ) = 0.99. i(max) (le régime permanent est pratiquement atteint).
III) Rupture du courant dans le circuit
On court-circuite la résistance
et l'inductance, la tension aux bornes de l'ensemble est nulle.
Loi des mailles :
Ldi/dt + R.i + r.i = 0
La solution de cette équation différentielle en i est de la forme:
i = A.ek.t
Les conditions initiales et la validité de cette expression quel que soit ‘t’ donne la solution suivante :
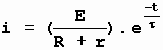
Unité :i (A); E(V) ; r,R (W ) ; L (H) ; t (s).
t = L/(R+r) est la constante de temps de la rupture du courant dans le circuit.
Détermination graphique de la constante de temps : Tracer la tangente à la courbe i = f(t). Elle coupe l'axe des temps en t = t.
IV) Energie emmagasinée par la bobine
1) Définition
L’énergie magnétique emmagasinée par une bobine d’inductance L parcourue par un courant d’intensité i est :
E = 0,5.L.i2
unité : L(H) ; E en joule(J) ; i en ampère (A) ;
2) Continuité du courant
L'énergie emmagasinée par la bobine ne peut varier brusquement. Or l'énergie est une fonction linéaire du carré de l'intensité du courant. Par conséquent l'intensité du courant dans une bobine est une fonction continue du temps: Il y a continuité du courant à travers une bobine.
Par contre il peut y avoir discontinuitéde la tension aux bornes d’une bobine lorsqu'on soumet par exemple un circuit RL à un échelon de tension .