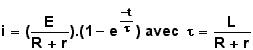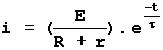Essentiel à retenir : systèmes électriques / compétences exigibles bac S

Chapitre 6 : dipôle RC

Le condensateur : un condensateur est constitué de 2 armatures séparées par un isolant. La tension u_AB aux bornes du condensateur est égale à la charge électrique q_A portée par l'armature 'A' divisée par la capacité C du condensateur (vidéo) :

Unités : C en farads (F); q_Aen coulomb (C); u_AB en volt (V); i en ampère(A).

Intensité du courant : l’intensité du courant entrant dans la borne A d’un condensateur est égale à la dérivée de la charge q_A par rapport au temps :

Réponse du dipôle RC à un échelon de tension (expérience)

animation : circuit RC

Avant l’instant t = 0 l'interrupteur est en position 2 le condensateur est déchargé. Puis à t = 0 on bascule l'interrupteur en position 1, le condensateur se charge.

Expression mathématique de u_C(t) (vidéo) . Dans un circuit série RC soumis à un échelon de tension E la loi des mailles donne :

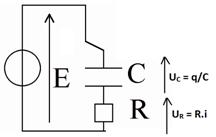E = R.i + u_c ; E = RC (du_c/dt) + u_c .

La solution de cette équation différentielle en u_c est :

Les conditions initiales et la validité de l'expression quel que soit l'instant 't' permettent de déterminer les constantes A et B et (vidéo)

Constante de temps du circuit RC : Par définition la constante de

temps tau du circuit RC série est égale au produit de la résistance R par la capacité C du condensateur :

Unité : la seconde (s) (démonstration vidéo).

Pour déterminer graphiquement tau on trace la tangente à la courbe u_c(t) en t = O. Cette tangente coupe l'asymptote u = E en un point M d'abscisse t =.

On peut également prendre le point M' de la courbe u_c(t) d'ordonnée 0,63.u(_max) = 0,63.E et d'abscisse t = .

Décharge d'un condensateur dans la résistance : expression mathématique de u_C (t) (vidéo)

Le condensateur étant chargé, on bascule l'interrupteur en position 2. Au cours de la décharge du condensateur la loi des mailles donne :

u_c+Ri = 0 donc u_c+RC.(du_c/dt) = 0

La solution de cette équation différentielle en u_c est de la forme:

Les conditions initiales et la validité de cette solution quelque soit l'instant 't' donnent la solution :

Pour déterminer graphiquement tau tracer la tangente à la courbe à t = 0 s. Cette droite coupe l'axe des abscisses en t = (vidéo).

Energie électrique E_eemmagasinée par un condensateur (vidéo): L'énergie électrique E_e emmagasinée par un condensateur de capacité C possédant une tension u à ses bornes et une charge q sur une des armatures est :

Unité: C en farad(F), u en volt(V), q en coulomb (C), E_e en joule (J).

Continuité de la tension aux bornes du condensateur : l'énergie du condensateur ne peut varier brusquement. Par conséquent la tension aux bornes d'un condensateur est continue au cours du temps. Il en va de même pour la charge q car q = C.u. Par contre l'intensité du courant i=dq/dt présente une discontinuité à la charge ou à la décharge.

chapitre 7 : dipôle RL

Tension aux bornes d’une bobine : une bobine ou solénoïde est constituée d’un enroulement de fil conducteur posé sur un support isolant. Soit une bobine de résistance ‘r’ et d’inductance L, lorsqu’elle est parcourue par un courant d’intensité i quelconque la tension à ses bornes est (voir schéma):

unité : U en volt(V) ; i en ampère(A) ; r en ohm() ; L en Henry(H) ;

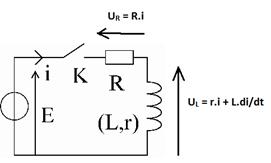
Etablissement du courant dans un circuit RL (expérience).

Animation

On considère un circuit comportant en série: un générateur parfait de f.e.m. E, un interrupteur, une bobine d'inductance L de résistance interne r, un conducteur ohmique de résistance R. A l'instant t = 0 on ferme l'interrupteur.

La loi des mailles donne (vidéo):

E = R.i + Ldi/dt + r.i

La solution de cette équation différentielle en i est de la forme : i = A + Be^k.t) .La condition initiale (i = 0) et la validité de cette expression quel que soit l'instant ‘t’ donnent la solution suivante (vidéo) :

est la constante de temps d’établissement du courant dans le circuit. Unités : i (A) ; E échelon de tension (V); r,R (); L(H); (s).

Détermination graphique de la constante de temps

Pour déterminer graphiquement , il suffit de tracer la tangente à la courbe i=f(t) à t = 0, celle ci coupe l’asymptote horizontale i = i(max) en un point M d’abscisse t = .

A t = l’intensité i() = 0,63.i(max)

à t = 5. , i(5. )= 0.99. i(max) (le régime permanent est pratiquement atteint).

Rupture du courant dans le circuit :

Animation

on court-circuite la résistance et l'inductance. La tension aux bornes de l'ensemble est alors nulle.

Loi des mailles :

Ldi/dt + R.i + r.i = 0

La solution de cette équation différentielle en i est de la forme:

i = A.e^k.t

Les conditions initiales et la validité de cette expression quel que soit ‘t’ donnent la solution suivante (vidéo):

Unité : i (A); E(V) ; r,R (W ) ; L (H) ; t, (s).

Pour déterminer graphiquement , tracer la tangente à l’origine celle ci coupe l’asymptote horizontale en t =

Energie emmagasinée par la bobine(vidéo). L’énergie magnétique E_m emmagasinée par une bobine d’inductance L parcourue par un courant d’intensité i est:

Unités : L(H) ; E en joule(J) ; i en ampère (A) ;

Continuité du courant : l'énergie emmagasinée par la bobine ne peut varier brusquement. Or l'énergie est une fonction linéaire du carré de l'intensité du courant. Par conséquent l'intensité du courant dans une bobine est une fonction continue du temps: Il y a continuité du courant dans un circuit contenant une bobine. Par contre il y a discontinuité de la tension aux bornes d’une bobine lorsqu'on soumet le circuit RL à un échelon de tension .

Chapitre 8 : circuit RLC

Décharge d'un condensateur dans un circuit RLC série (expérience)

Animation

Un condensateur chargé par un générateur de force électromotrice E se décharge dans un circuit comportant une bobine d'inductance L (de résistance négligeable), en série avec une résistance R. Pour charger le condensateur on place l'interrupteur en position 1. Pour le décharger on place l'interrupteur en position 2.
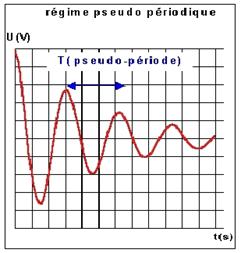
Le régime pseudo périodique. Pour des valeurs faibles de résistance, la décharge du condensateur dans un circuit RLC est oscillante amortie. Elle est pseudo périodique de pseudo période T. Il ne s'agit pas d'une oscillation périodique car l'amplitude des oscillations u_mdiminue au cours du temps.

Le régime apériodique : Pour une résistance trop importante, il n'y a plus d'oscillation avant d'atteindre le régime permanent. La tension aux bornes du condensateur tend vers O volt sans osciller.

Pseudo période T (vidéo) : pour une faible valeur de résistance, la pseudo période T est peu différente de la période propre du circuit To (période d'oscillation de la tension dans le cas d'un régime périodique ) :

unité : L(H) ; C(F) ; T,To(s)

Oscillateur non amorti : régime périodique. On reprend un schéma identique au précédent. On charge le condensateur sous une tension E, puis on le décharge dans la bobine. Si la résistance dans le circuit est nulle, la décharge est oscillante non amortie, il s'agit du régime périodique, de période propre:

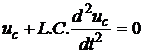
Expression u_c= f(t) (vidéo) La tension u_c aux bornes du condensateur dans le circuit LC série est solution de l'équation différentielle du second ordre :

La solution de ce type d'équation est ( video) :

Aspect énergétique, oscillateur non amorti (vidéo)

Animation

Soit un condensateur possédant une énergie électrique

Ee = ½.C.U_c² en série avec une bobine possédant une énergie magnétique Em = ½ L.i². L'énergie totale emmagasinée par le circuit est égale à la somme de Ee et Em. L'énergie totale est constante car il n'y a pas de perte d'énergie :

E = Em+Ee = 1/2L.i²+1/2.C.U_c²

Oscillateur amorti, régime pseudo périodique : le circuit contient maintenant une résistance R. L'énergie totale d'un circuit RLC série diminue. En effet de l'énergie est perdue par effet joule dissipation sous forme de chaleur ). Ee(max) et Em(max) diminue progressivement jusqu'à devenir nulle. Pour annuler le terme d'amortissement dû à la résistance il faut placer dans le circuit un montage dit à "résistance négative".

Grille de compétences Avant chaque ds inscrire dans la case acquis* si la compétence est maitrisée ou non et rendre avec le DM les définitions à connaître.*
Compétences exigibles au baccalauréat				Acquis	définitions	exercices
6. Dipôle RC	Connaître la représentation symbolique d'un condensateur.
	En utilisant la convention récepteur, savoir orienter un circuit sur un schéma, représenter les différentes flèches tension, noter les charges des différentes armatures du condensateur.
	Connaître les relations charge-intensité et charge-tension pour un condensateur en convention récepteur; connaître la signification de chacun des termes et leur unité. Savoir exploiter la relation q = C.u
	1.2. Le dipôle RC Effectuer la résolution analytique pour la tension aux bornes du condensateur ou la charge de celui-ci lorsque le dipôle est soumis à un échelon de tension.
	En déduire l'expression de l'intensité dans le circuit.
	Connaître l'expression de la constante de temps et savoir vérifier son unité par analyse dimensionnelle.
	Connaître l'expression de l'énergie emmagasinée dans un condensateur.
	Savoir que la tension aux bornes d'un condensateur n'est jamais discontinue. Savoir exploiter un document expérimental pour : -identifier les tensions observées. -montrer l'influence de R et de C sur la charge ou la décharge.
	Savoir-faire expérimentaux
	Réaliser un montage électrique à partir d'un schéma.
	Réaliser les branchements pour visualiser les tensions aux bornes du générateur, du condensateur et du conducteur ohmique.
	Montrer l'influence de l'amplitude de l'échelon de tension, de la résistance et de la capacité sur le phénomène observé lors de la charge et de la décharge du condensateur.
Compétences exigibles au baccalauréat				Acquis	définitions	exercices
7. le dipôle RL
		Effectuer la résolution analytique pour l'intensité du courant dans un dipôle RL soumis à un échelon de tension.
		En déduire la tension aux bornes de la bobine.
		Connaître l'expression de la constante de temps et savoir vérifier son unité par analyse dimensionnelle.
		Connaître l'expression de l'énergie emmagasinée.
		Savoir qu'une bobine s'oppose aux variations du courant du circuit où elle se trouve et que l'intensité de ce courant ne subit pas de discontinuité.
		Savoir exploiter un document expérimental pour: - identifier les tensions observées - montrer l'influence de R et de L lors de l'établissement et de la disparition du courant - déterminer une constante de temps.
		Savoir-faire expérientaux Réaliser un montage électrique à partir d'un schéma. Réaliser les branchements pour visualiser les tensions aux bornes du générateur, de la bobine et du conducteur ohmique supplémentaire. Montrer l'influence de l'amplitude de l'échelon de tension, de R et de L sur le phénomène observé.
Compétences exigibles au baccalauréat			Acquis		définitions	exercices
8. circuit RLC		Définir et reconnaître les régimes périodique, pseudo-périodique et apériodique.
		Savoir tracer l'allure de la tension aux bornes du condensateur en fonction du temps pour les régimes périodique, pseudo-périodique et apériodique.
		Dans le cas d'un amortissement négligeable, effectuer la résolution analytique pour la tension aux bornes du condensateur ou la charge de celui-ci.
		En déduire l'expression de l'intensité dans le circuit.
		Connaître l'expression de la période propre, la signification de chacun des termes et leur unité.
		Savoir que le dispositif qui entretient les oscillations fournit l'énergie évacuée par transfert thermique.
		Savoir interpréter en terme d'énergie les régimes périodique, pseudo-périodique, apériodique et entretenu.
		Savoir exploiter un document expérimental pour: -identifier les tensions observées, -reconnaître un régime, -montrer l'influence de R et de L ou C sur le phénomène d'oscillations, -déterminer une pseudo-période.
		Savoir-faire expérimentaux
		réaliser un montage électrique à partir d'un schéma.
		Réaliser les branchements pour visualiser les tensions aux bornes du condensateur et de la résistance supplémentaire éventuelle.
		Montrer l'influence de R, L et C sur le phénomène observé.
		Mesurer une pseudo-période et une période.
		Utiliser un oscilloscope: -le régler: mode de balayage, finesse du trait, réglage du "zéro", choix de la sensibilité verticale et choix d'une base de temps, sélection des voies; -repérer les tensions observables simultanément dans un circuit; -visualiser l'image d'une intensité; -visualiser simultanément deux tensions.