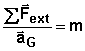les 3 lois de newton

IV) évolution des systèmes mécaniques

chapitre 11 : mouvement dans un champ de pesanteur uniforme

chapitre 12 : mouvement des satellites et des planètes

Chapitre 9 : les 3 lois de Newton

compétence exigibles au bac

1. La mécanique de Newton
Choisir un système.
Choisir les repères d'espace et de temps.
Faire l'inventaire des forces extérieures appliquées à ce système.
Définir le vecteur accélération et exploiter cette définition, connaître son unité.
Enoncer les trois lois de Newton.
Savoir exploiter un document expérimental (série de photos, film, acquisition de données avec un ordinateur...): reconnaître si le mouvement du centre d'inertie est rectiligne uniforme ou non, déterminer des vecteurs vitesse et accélération, mettre en relation accélération et somme des forces, tracer et exploiter des courbes v = f(t).
Savoir faire expérimentaux
Savoir enregistrer expérimentalement le mouvement de chute d'un solide dans l'air et/ou dans un autre fluide en vue de l'exploitation du document obtenu.

Rappel de mécanique

Effet d'une force sur un système matériel :Un système matériel est un solide(ou un ensemble de solides) dont on étudie le mouvement. Les trois effets principaux d'une force sur un système matériel sont :

1) déformation du système

2) mise en mouvement du système

3) modification de son mouvement

Solide pseudo-isolé et isolé Un solide est pseudo-isolé si la somme vectorielle des forces extérieures qui agissent sur lui est égale au vecteur nul.

Le solide est isolé si aucune force ne s'exerce sur lui.

unité: P en Newton(N), m en kilogramme (kg), g intensité du champ de pesanteur terrestre (N.kg^-1).

La poussée d'Archimède Tout corps plongé dans un fluide subit de sa part une force appelée poussée d'Archimède, de norme . La norme de cette force est égale ou poids du volume de fluide déplacé par ce corps. La poussée d'Archimède est égale à l'opposé du vecteur poids de fluide déplacé :

Caractéristiques de la poussée d'Archimède : direction : verticale ;sens : opposé au vecteur poids du solide point d'application : G ; norme : =m_{(fluide déplacé}).g

Référentiel, repère : un référentiel d'étude est un solide par rapport auquel on étudie le mouvement du système matériel. Dans un référentiel donné, on peut définir une infinité de repères d'espace. Ils sont constitués généralement de trois vecteurs unitaires orthogonaux et d'un point origine. Exemple repère cartésien R orthonormé :

Première loi de Newton : principe d'inertie Dans un référentiel galiléen, le centre d'inertie d'un système matériel isolé ou pseudo-isolé est soit immobile, soit en mouvement rectiligne uniforme. Son vecteur vitesse, de valeur v_G , est constant. La réciproque est vraie.

Troisième loi de Newton, principe d'interaction : Lorsqu'un système matériel A exerce une force sur un système matériel B alors celui-ci exerce sur le système matériel A une force opposée Les droites d'action des 2 forces sont confondues:

Vecteur champ de pesanteur uniforme : Dans un cube de volume V = 1 km³ on peut considérer que le vecteur champ de pesanteur terrestre (de norme g) est constant : il garde ses 3 caractéristiques (sens, direction, norme) identiques. Le vecteur poids Le vecteur poids est égal au produit de la masse 'm' de l'objet par le vecteur champ de pesanteur terrestre :

Le vecteur accélération du centre d'inertie : Le vecteur accélération instantanée du centre d'inertie d'un solide est égal à la variation du vecteur vitesse instantanée divisée par l'intervalle de temps dt pendant lequel s'effectue cette variation. Le vecteur accélération est égal à la dérivée du vecteur vitesse par rapport au temps. exemple de calcul de la valeur de l’accélération

Caractéristiques du vecteur accélération :

1) une direction : celle du vecteur

2) un sens : celui de du vecteur

3) une norme : a_G

4) un point d'application: le point de la trajectoire où se trouve le point G à l'instant t.

L'unité d'accélération est le m.s^-2.

Seconde loi de Newton Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquée à un système matériel, est égale au produit de sa masse par le vecteur accélération de son centre d'inertie : (vidéo)

Rôle de la masse : D'après la seconde loi de Newton on peut affirmer que pour une somme vectorielle de force constante, plus la masse est importante plus l'accélération est faible. En effet :

La masse s'oppose à la variation de vitesse. Plus la masse d'un corps est importante plus son inertie est importante : la masse correspond à de l'inertie mécanique.

Chapitre 10 : chute verticale

compétence exigibles au bac

Les 2 régimes d'une chute verticale : au cours d'une chute verticale on distingue deux régimes:

Le régime transitoire pendant lequel la vitesse augmente.

Le régime permanent pendant lequel la vitesse reste constante.

Cette vitesse est appelée vitesse limite, notée v(limite). Dans le cas d'une force de frottement fluide de valeur f = k.v on définit le temps caractéristique. Celui ci correspond à l'abscisse du point d’intersection entre la tangente à la courbe v(t) à l'instant t = 0 s, et l'asymptote d'équation v = v(limite).

Etude mécanique

Pour effectuer une étude mécanique d'un objet en mouvement il faut définir (vidéo):

1) le système : la bille.

2) le référentiel : la terre supposée référentiel galiléen.

3) le repère (cartésien dans notre cas) lié au référentiel

4) définir la somme des forces extérieures agissant sur le système :

: vecteur poids de l'objet ;: poussée d'Archimède (vidéo) ; : force de frottement fluide

Force de frottement fluide :L'ensemble des forces de frottement entre le solide et le fluide est modélisé par une seule force.Il existe plusieurs types de force de frottement fluide. Si l'objet est petit et que sa vitesse par rapport au fluide est faible, alors le fluide s'écoule sous forme de couches continue autour de l'objet. Il s'agit d'un écoulement laminaire. On parle alors de force de frottement laminaire. Une force de frottement laminaire est égale à l'opposé du produit du coefficient de frottement fluide laminaire h par le vecteur vitesse du centre d'inertie du solide :

h: coefficient de frottement fluide laminaire (kg.s^-1), qui dépend de la forme, de la taille de l'objet et du type de fluide (notamment de sa viscosité).

Si l'objet est gros et que sa vitesse par rapport au fluide est importante, le fluide s'écoule de façon turbulente. Dans le cas d'une force de frottement fluide turbulent :

;

: coefficient de frottement turbulent (kg.m^-1).v : vitesse du solide(m.s^-1). f : force de frottement fluide turbulent (N). De manière générale la force de frottement est opposée à la vitesse, et sa norme est de la forme : f = A.vⁿ

Equation différentielle du mouvement (vidéo). La seconde loi de Newton donne, dans le cas d'une chute libre avec force de frottement laminaire, l'équation différentielle en z(position du centre d'inertie de la bille sur l'axe vertical orienté vers le bas) :

'mf' : masse de fluide déplacé(kg): 'm' masse de la bille(kg) ; 'h' coefficient de frottement laminaire (kg.s^-1) ; g_z: coordonnée du vecteur champ de pesanteur sur l'axe des z : g_z= 9,8 N.kg^-1.

méthode d'Euler (vidéo) . Pour que le calcul numérique de la vitesse, de l'accélération et de la position soit proche de l'expérience il faut prendre un pas environ 10 fois inférieur au temps tau caractéristique :

Chute libre Un objet est en chute libre quand il n'est soumis qu'à son poids. Ce cas de figure n'est réalisable que si le solide tombe dans le vide !

Equations horaires du mouvement (vidéo). En utilisant la seconde loi de Newton, on obtient les résultats suivants (axe des z orienté vers le centre de la terre): Avec C1 = Vo_z et C2 = z_o , constantes déterminées avec les conditions initiales

Chapitre 11 : mouvement dans un champ de pesanteur uniforme

compétences exigibles au bac (chapitre 11 et 12)

2.2. Mouvements plans
-Mouvement de projectiles dans un champ de pesanteur uniforme

Appliquer la deuxième loi de Newton à un projectile dans un champ de pesanteur uniforme.
Montrer que le mouvement est plan.
établir l'équation de la trajectoire à partir des équations horaires paramétriques.
Savoir exploiter un document expérimental reproduisant la trajectoire d'un projectile: tracer des vecteurs vitesse et accélération, trouver les conditions initiales.
Savoir-faire expérimentaux
Savoir enregistrer expérimentalement la trajectoire d'un projectile et exploiter le document obtenu.

Seconde loi de Newton (ou principe fondamental de la dynamique : La somme des forces extérieures appliquées sur le centre d'inertie du solide de masse 'm' dans un référentiel galiléen, est égale au produit de la masse par le vecteur accélération du centre d'inertie G la poussée d’Archimède et les forces de frottements sont négligées) (vidéo) :

L'accélération d'un projectile dans un champ de pesanteur constant est donc une accélération uniforme. Le mouvement du centre d'inertie du projectile ne dépend pas de sa masse, mais uniquement des conditions initiales (vitesse et position).

Equation différentielle du mouvement : (vidéo)

: vecteur vitesse initiale du projectile. Le vecteur position du centre d'inertie est, dans le repère orthonormé cartésien orientant respectivement les axes x, y, z :

Le vecteur vitesse du centre d'inertie G du solide est égal à la dérivée du vecteur position par rapport au temps :

De même le vecteur accélération du centre d'inertie du solide est égal à la dérivée du vecteur vitesse par rapport au temps :

D'après la seconde loi de Newton :

Equations horaires du mouvement (vidéo). Dans le repère cartésien

La condition initiale sur la vitesse est :

v_0y La condition initiale sur la position est : G(x_0 ; y₀)

Par conséquent :

v_x = v_0x ;v_y = –g.t + v_oy

x = v_0x.t + x_{0
;} y = –0,5.g.t² + v_0y.t + y_o

Equation cartésienne de la trajectoire (vidéo) L'équation cartésienne de la trajectoire est la relation liant les coordonnées du point G(x,y,z). En éliminant le temps dans les équations horaires du mouvement on obtient les équations cartésiennes de la trajectoire. La trajectoire s'inscrit dans le plan (y,O,z). C'est une parabole.

La flèche H et la portée D Suivant les conditions initiales la forme de la trajectoire est modifiée.

On appelle portée D la distance maximale parcourue sur l'axe horizontal, le projectile étant projeté à une altitude z. Le projectile touche le sol au point P (y_P ; z_P = 0). En utilisant l'équation cartésienne, on remplace z = z_P = 0, et on en déduit la valeur de y_P, qui correspond à la portée D.

La flèche correspond à l'altitude la plus élevée atteinte par le projectile (calculée à partir de l'altitude initiale zo).

Chapitre 12 : mouvement des satellites et des planètes

Les lois de Kepler

1^ière loi ou loi des orbites elliptiques 1605 Toutes les orbites des planètes sont des ellipses dont le soleil occupe l'un des foyers.

2^nd loi ou loi des aires (1604) Pendant des intervalles de temps égaux Dt la planète balaye des surfaces 'S' de l'ellipse égales.
Si Dt = t₁-t₀= t₃-t₂ alors S1 = S2

3^ième loi ou loi des périodes La période de révolution(vidéo) au carré divisée par le demi-grand axe 'a' au cube est une constante.
Elle ne dépend pas de la planète mais uniquement de la masse M_S du Soleil et de la constante d'attraction universelle G :

G = 6,67.10^-11N.kg^-2.m²;M_S= 1,96.10³⁰kg.

Force d’attraction gravitationnelle (vidéo) Un corps ponctuel A de masse m_Aexercesur un corps ponctuel B de masse m_Bune force d'attraction gravitationnelle telle que :

L'expression de cette force d'attraction gravitationnelle s'applique également pour des objets à symétrie sphérique, pour lesquelles la matière est répartie uniformément dans toutes les directions. La force gravitationnelle s'applique alors au centre d'inertie du solide.

Le mouvement circulaire uniforme (vidéo) : La base de Frénet Dans le cas des mouvements circulaires on n'utilise pas le repère cartésien, mais le repère de Frenet, défini par deux vecteurs orthonormés dans le plan :

Soit un point P mobile décrivant une trajectoire curviligne la base de Frénet à l'instant t est :

: vecteur unitaire tangent à la trajectoire au point P, orienté généralement dans le sens du mouvement ; vecteur unitaire, normal à la trajectoire, et centripète.

Vecteur accélération pour un mouvement circulaire uniforme (vidéo) Pour un mouvement circulaire uniforme de rayon de trajectoire R, le vecteur accélération et le vecteur vitesse d'un point mobile sont :

L'accélération est centripète ( orientée vers le centre de la trajectoire).

Vitesse et accélération du centre d'inertie d'une planète, dans le cas d'un mouvement circulaire uniforme En terminale, on considèrera que les orbites sont circulaires. Dans le cas d'un mouvement circulaire uniforme les vecteurs vitesse et accélération du centre d'inertie sont:

(vidéo):

Démonstration prouvant que le mouvement est circulaire uniforme clique ici.

Dans le cas particulier du mouvement circulaire uniforme, la période de révolution de la planète autour du soleil est :

Satellites de la terre en mouvement circulaire uniforme Le mouvement des satellites se fait dans un plan contenant le centre d'inertie de la terre G_T. En effet la force de gravitation exercée par la terre sur le satellite est centripète.

La vitesse et la période d'un satellite décrivant une orbite circulaire à l’altitude h, centrée sur le centre d'inertie de la Terre, sont :

h: altitude du satellite(m); R_T= 6400 km rayon de la terre. m_T= 6.10²⁴kg , masse de la terre. G = 6,67.10^-11N.kg^-2.m² constante de gravitation universelle.

Satellite géostationaire Un satellite est géostationnaire s'il est toujours situé au-dessus du même point de la terre.

Il est immobile dans un référentiel terrestre. Comme son plan orbital doit contenir le centre de la terre, son orbite est dans le plan de l'équateur. Sa période de révolution T est égale à la période de rotation de la terre dans le référentiel géocentrique. Cette période est appelée également jour sidéral. T =23 h 56 min 4 s = 86164 s.

Compétences exigibles au baccalauréat

1. La mécanique de Newton
2. étude de cas
2.1. Chute verticale d'un solide
   Chute verticale avec frottement
   Chute verticale libre
2.2. Mouvements plans
    -Mouvement de projectiles dans un champ de pesanteur uniforme
    -Satellites et planètes
3. Systèmes oscillants
3.1. Présentation de divers systèmes oscillants mécaniques
3.2. Le dispositif solide-ressort
3.3. Le phénomène de résonance
4. Aspects énergétiques
5. L'atome et la mécanique de Newton: ouverture au monde quantique

2. étude de cas
2.1. Chute verticale d'un solide Résumé
Définir un champ de pesanteur uniforme.
Connaître les caractéristiques de la poussée d'Archimède. animation Flash
Chute verticale avec frottement
Appliquer la deuxième loi de Newton à un corps en chute verticale dans un fluide et établir l'équation différentielle du mouvement, la force de frottement étant donnée.
Connaître le principe de la méthode d'Euler pour la résolution approchée d'une équation différentielle.
Chute verticale libre
Définir une chute libre, établir son équation différentielle et la résoudre.
Définir un mouvement rectiligne uniformément accéléré.
Savoir exploiter des reproductions d'écrans d'ordinateur (lors de l'utilisation d'un tableur grapheur) correspondant à des enregistrements expérimentaux.
Savoir exploiter des courbes v =f(t) pour :
-reconnaître le régime initial et/ou le régime asymptotique
-évaluer le temps caractéristique correspondant au passage d'un régime à l'autre
-déterminer la vitesse limite Applet Java
Dans le cas de la résolution par méthode itérative de l'équation différentielle, discuter de la pertinence des courbes obtenues par rapport aux résultats expérimentaux (choix du pas de résolution, modèle proposé pour la force de frottement)
Savoir-faire expérimentaux
Utiliser un tableur ou une calculatrice pour résoudre une équation différentielle par la méthode d'Euler.
2.2. Mouvements plans
-Mouvement de projectiles dans un champ de pesanteur uniforme Résumé
Appliquer la deuxième loi de Newton à un projectile dans un champ de pesanteur uniforme. Applet Java
Montrer que le mouvement est plan.
établir l'équation de la trajectoire à partir des équations horaires paramétriques.
Savoir exploiter un document expérimental reproduisant la trajectoire d'un projectile: tracer des vecteurs vitesse et accélération, trouver les conditions initiales. Animation Flash
Savoir-faire expérimentaux
Savoir enregistrer expérimentalement la trajectoire d'un projectile et exploiter le document obtenu.
-Satellites et planètes
Enoncer les lois de Kepler et les appliquer à une trajectoire circulaire ou elliptique. (Animation Flash Université du Nebraska)
Définir un mouvement circulaire uniforme et donner les caractéristiques de son vecteur accélération. Applet Cabri Java
Connaître les conditions nécessaires pour observer un mouvement circulaire uniforme: vitesse initiale non nulle et force radiale.
Enoncer la loi de gravitation universelle sous sa forme vectorielle pour des corps dont la répartition des masses est à symétrie sphérique et la distance grande devant leur taille.
Appliquer la deuxième loi de Newton à un satellite ou à une planète.
Démontrer que le mouvement circulaire et uniforme est une solution des équations obtenues en appliquant la deuxième loi de Newton aux satellites ou aux planètes.
Définir la période de révolution et la distinguer de la période de rotation propre.
Exploiter les relations liant la vitesse, la période de révolution et le rayon de la trajectoire.
Connaître et justifier les caractéristiques imposées au mouvement d'un satellite pour qu'il soit géostationnaire.
Retrouver la troisième loi de Kepler pour un satellite ou une planète en mouvement circulaire uniforme.
Exploiter des informations concernant le mouvement des satellites ou des planètes.

3. Systèmes oscillants
3.1. Présentation de divers systèmes oscillants mécaniquesRésumé

Définir un pendule simple. (Animation Flash pendule simple du site Enargeia)
Justifier la position d'équilibre dans le cas d'un pendule simple. (Animation Flash : forces, vitesse, accélération : pendule simple)
Définir l'écart à l'équilibre, l'abscisse angulaire, l'amplitude, la pseudo-période, la période propre et les mesurer sur un enregistrement.
Enoncer la loi d'isochronisme des petites oscillations. (Animation Flash : isochronisme)
Savoir comment un système peut atteindre un régime apériodique.
Savoir que dans le cas d'un amortissement faible, la pseudo-période est voisine de la période propre.
Pour un pendule simple, justifier la forme de l'expression de la période propre par analyse dimensionnelle.
A partir d'une série de résultats expérimentaux, vérifier la validité de l'expression de la période propre d'un pendule simple.
Savoir-faire expérimentaux
Décrire un protocole expérimental permettant:
- d'enregistrer le mouvement d'un système oscillant plus ou moins amorti
- de vérifier la loi d'isochronisme des petites oscillations
- de vérifier l'expression de la période propre dans le cas d'un pendule simple.
3.2. Le dispositif solide-ressort
Connaître les caractéristiques de la force de rappel exercée par un ressort. (Animation Flash Oscillateur horizontal du site Enargeia) ou Animation de G.Tulloue
Appliquer la deuxième loi de Newton au solide et effectuer la résolution analytique dans le cas d'un dispositif oscillant horizontalement.
Connaître la signification de tous les termes intervenant dans la solution de l'équation différentielle et leur unité.Animation Flash Oscillateur horizontal (Site perso de F.Passebon)
Connaître er savoir exploiter l'expression de la période propre, vérifier son homogénéité par analyse dimensionnelle.
Savoir-faire expérimentaux
Enregistrer un mouvement oscillant amorti.
Savoir mesurer une amplitude, une pseudo-période.
Savoir faire varier l'amortissement.
Savoir montrer l'influence des paramètres masse et rigidité sur la période propre.
3.3. Le phénomène de résonance
Savoir que la résonance mécanique se produit lorsque la période de l'excitateur est voisine de la période propre du résonateur.
Savoir que l'augmentation de l'amortissement provoque une diminution de l'amplitude.
Connaître des exemples de résonance mécanique. (vidéo Pont de Tacoma, vidéo résonance d'un verre: Université de Salford , animation flash résonance amortisseurs d'une voiture )

5. L'atome et la mécanique de Newton: ouverture au monde quantique Résumé
Connaître les expressions de la force d'interaction gravitationnelle et de la force d'interaction électrostatique.
Savoir que l'énergie de l'atome est quantifiée et que la mécanique de Newton ne permet pas d'interpréter cette quantification.
Connaître et exploiter la relation , connaître la signification de chaque terme et leur unité.
Convertir les joules en eV et réciproquement.
Interpréter un spectre de raies.
Dans les échanges d'énergie, associer le MeV au noyau et l'eV au cortège électronique.