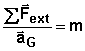Chapitre 9 :
les 3 lois de Newton) Rappel de mécanique
Rappel
de mécanique
Effet d'une force sur un système matériel :Un système matériel est un
solide(ou un ensemble de solides) dont on étudie le mouvement. Les trois effets
principaux d'une force sur un système matériel sont :
1) déformation du système
2) mise en mouvement du système
3) modification de son mouvement
Solide pseudo-isolé et isolé Un solide
est pseudo-isolé si la somme vectorielle des forces extérieures qui agissent
sur lui est égale au vecteur nul.
Le solide est isolé si aucune force ne s'exerce sur lui.
Référentiel, repère : un référentiel d'étude est
un solide par rapport auquel on étudie le mouvement du système matériel. Dans un référentiel donné, on peut définir une
infinité de repères d'espace. Ils sont constitués généralement de trois
vecteurs unitaires orthogonaux et d'un point origine. Exemple de repère cartésien R orthonormé :
Première loi de Newton : principe
d'inertie Dans
un référentiel galiléen, le centre d'inertie d'un système matériel isolé ou
pseudo-isolé est soit immobile, soit en mouvement rectiligne uniforme. Son
vecteur vitesse, de valeur vG , est
constant. La réciproque est vraie.
Troisième loi de Newton, principe d'interaction : Lorsqu'un système matériel A exerce une force sur un
système matériel B alors celui-ci exerce sur le système matériel A une force
opposée Les droites d'action des 2 forces sont confondues:
Vecteur champ de pesanteur uniforme : Dans un cube de volume V =
1 km3 on peut considérer que le vecteur champ de pesanteur terrestre
(de norme g) est constant : il garde ses 3
caractéristiques (sens, direction, norme) identiques.
Le vecteur poids
Le vecteur poids est égal au produit de la masse 'm' de l'objet par le
vecteur champ de pesanteur terrestre :
unité: P en Newton(N), m en kilogramme (kg), g intensité du champ de
pesanteur terrestre (N.kg-1).
3) La poussée
d'Archimède
Tout corps plongé dans un fluide subit de sa part une force appelée
poussée d'Archimède, de norme 
.
La norme de cette force est égale ou poids du volume de
fluide déplacé par ce corps. La poussée d'Archimède est égale à l'opposé
du vecteur poids de fluide déplacé :
Caractéristiques de la poussée d'Archimède :
direction : verticale
sens : opposé au vecteur poids du
solide
point d'application : G
norme : =m(fluide déplacé).g
Le vecteur accélération du centre d'inertie : Le vecteur accélération instantanée du centre
d'inertie d'un solide est égal à la variation du vecteur vitesse instantanée
divisée par l'intervalle de temps dt pendant lequel
s'effectue cette variation. Le vecteur accélération
est égal à la dérivée du vecteur vitesse par rapport au temps. exemple de calcul de la valeur
de l’accélération
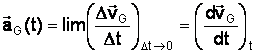
Caractéristiques
du vecteur accélération :
1) une
direction : celle du vecteur 
2) un sens :
celui de du vecteur 
4) un point
d'application: le point de la trajectoire où se trouve le point G à l'instant
t.
L'unité
d'accélération est le m.s-2.
Seconde loi de Newton Dans un référentiel
galiléen, la somme vectorielle des forces extérieures appliquée à un système
matériel, est égale au produit de sa masse par le vecteur accélération de son
centre d'inertie : (vidéo)
Chapitre 10 :
chute verticale
Les 2 régimes d'une chute verticale : au cours d'une chute verticale on distingue deux
régimes:
Le régime transitoire pendant lequel la vitesse augmente.
Le régime permanent pendant lequel la
vitesse reste constante.
Cette vitesse est appelée vitesse limite, notée v(limite). Dans le cas d'une
force de frottement fluide de valeur f = k.v on
définit le temps 
caractéristique. Celui ci correspond à l'abscisse du
point d’intersection entre la tangente à la courbe v(t) à l'instant t = 0
s, et l'asymptote d'équation v = v(limite).
Etude mécanique
Pour effectuer une étude mécanique d'un objet en mouvement il faut
définir (vidéo):
1) le système : la bille.
2) le référentiel : la terre supposée référentiel galiléen.
3) le repère (cartésien dans notre cas) lié au référentiel 
4) définir la somme des forces extérieures agissant sur le système :
: vecteur
poids de l'objet ;
: poussée
d'Archimède (vidéo) ; 
: force
de frottement fluide
Force de frottement fluide :L'ensemble des forces de frottement entre le
solide et le fluide est modélisé par une seule force.Il
existe plusieurs types de force de frottement fluide. Si l'objet est petit et que sa vitesse par
rapport au fluide est faible, alors le fluide s'écoule sous forme de couches
continue autour de l'objet. Il s'agit d'un écoulement
laminaire. On parle alors de force de frottement
laminaire. Une force de frottement laminaire est égale à l'opposé du produit du
coefficient de frottement fluide laminaire h par le vecteur vitesse du centre
d'inertie du solide : 
h: coefficient de
frottement fluide laminaire (kg.s-1), qui
dépend de la forme, de la taille de l'objet et du type de fluide (notamment de
sa viscosité).
Si l'objet est gros et que sa vitesse par rapport
au fluide est importante, le fluide s'écoule de façon turbulente. Dans le cas
d'une force de frottement fluide turbulent : 
: coefficient de
frottement turbulent (kg.m-1).
v : vitesse du solide(m.s-1).
f : force de frottement fluide turbulent (N).
De manière générale la force de frottement est
opposée à la vitesse, et sa norme est de la forme : f = A.vn
Equation différentielle du mouvement (vidéo). La seconde loi de Newton donne, dans le cas
d'une chute libre avec force de frottement laminaire, l'équation différentielle
en z(position du centre d'inertie de la bille sur l'axe vertical orienté vers
le bas) :
'mf' : masse de
fluide déplacé(kg): 'm' masse de la bille(kg) ; 'h' coefficient de frottement
laminaire (kg.s-1) ; gz:
coordonnée du vecteur champ de pesanteur sur l'axe des z : gz = 9,8 N.kg-1.
méthode d'Euler
(vidéo) . Pour que le calcul numérique de la vitesse, de
l'accélération et de la position soit proche de l'expérience il faut prendre un
pas environ 10 fois inférieur au temps t caractéristique : 
Chute libre
Un objet est en chute libre quand il n'est
soumis qu'à son poids. Ce cas de figure n'est réalisable que si le solide tombe
dans le vide !
Equations horaires du mouvement (vidéo). En utilisant la seconde loi de Newton, on obtient
les résultats suivants (axe des z orienté vers le centre de la terre):
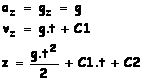
Avec C1 = Voz et C2 = zo , constantes déterminées avec les conditions
initiales.
Chapitre 11 :
mouvement dans un champ de pesanteur uniforme
Seconde loi de Newton (ou principe
fondamental de la dynamique : La
somme des forces extérieures appliquées sur le centre d'inertie du solide de
masse 'm' dans un référentiel galiléen, est égale au produit de la masse par le
vecteur accélération du centre d'inertie G la poussée d’Archimède et les
forces de frottements sont négligées) (vidéo) :
L'accélération d'un projectile dans un champ de pesanteur constant est
donc une accélération uniforme. Le mouvement du centre d'inertie du projectile ne dépend pas de sa masse,
mais uniquement des conditions initiales (vitesse et position).
Equation différentielle du mouvement : (vidéo)
: vecteur vitesse initiale du projectile. Le vecteur position du centre d'inertie est, dans le
repère orthonormé 
cartésien orientant
respectivement les axes x, y, z : 
Le vecteur vitesse du centre d'inertie G du solide est égal à la dérivée
du vecteur position par rapport au temps :
De même le vecteur accélération du centre d'inertie du solide est égal à
la dérivée du vecteur vitesse par rapport au temps :
D'après la seconde loi de
Newton :
Equations
horaires du mouvement (vidéo). Dans
le repère cartésien 
La condition initiale
sur la vitesse est : vx
= v0x ; vy = –g.t + v0y
La condition initiale sur la position est : G(x0 ;
y0) donc x = v0x.t
+ x0 et y = –0,5.g.t² + v0y.t + yo
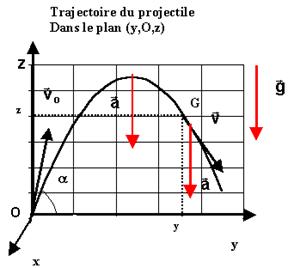
Equation
cartésienne de la trajectoire (vidéo) L'équation cartésienne de la trajectoire est la
relation liant les coordonnées du point G(x,y,z). En éliminant le temps dans les équations horaires du
mouvement on obtient les équations cartésiennes de la trajectoire. La
trajectoire s'inscrit dans le plan (y,O,z). C'est une parabole.
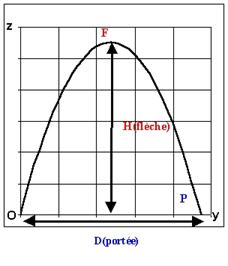La
flèche H et la portée D Suivant
les conditions initiales la forme de la trajectoire est modifiée.
On appelle portée D la distance maximale
parcourue sur l'axe horizontal, le projectile étant projeté à une
altitude z. Le projectile touche le sol au point P (yP
; zP = 0). En utilisant l'équation cartésienne, on remplace z =
zP = 0, et on en déduit la valeur de yP, qui correspond à la portée D.
La flèche correspond à l'altitude la plus élevée atteinte par le
projectile (calculée à partir de
l'altitude initiale zo).
Chapitre 12 : mouvement des satellites et des planètes
Les
lois de Kepler
1ière loi ou loi des orbites elliptiques 1605 Toutes les orbites des
planètes sont des ellipses dont le soleil occupe l'un des foyers.
2nd loi ou loi des aires (1604) Pendant des intervalles de temps égaux Dt la planète balaye des surfaces 'S' de l'ellipse égales.
Si Dt = t1-t0 = t3-t2 alors S1 = S2
3ième loi ou loi des périodes La période de révolution (vidéo) au carré
divisée par le demi-grand axe 'a' au cube est une constante.
Elle ne dépend pas de la planète mais
uniquement de la masse MS du Soleil et de la constante d'attraction
universelle G :
G = 6,67.10-11N.kg-2.m2 ;MS =
1,96.1030 kg.
Force d’attraction
gravitationnelle (vidéo) Un corps ponctuel A de masse mA exerce
sur un corps ponctuel B de masse mB
une force d'attraction gravitationnelle telle que :
L'expression de cette force d'attraction gravitationnelle s'applique
également pour des objets à symétrie sphérique, pour lesquelles la
matière est répartie uniformément dans toutes les directions. La force
gravitationnelle s'applique alors au centre d'inertie du solide.
Le mouvement circulaire uniforme (vidéo) : La base de Frénet Dans le cas des mouvements circulaires on n'utilise
pas le repère cartésien, mais le repère de Frenet,
défini par deux vecteurs orthonormés dans le plan : 
Soit un point P mobile décrivant une trajectoire curviligne la base de Frénet à l'instant t est :
: vecteur unitaire
tangent à la trajectoire au point P, orienté généralement dans le sens du
mouvement ;
vecteur unitaire, normal à la trajectoire, et
centripète.
Vecteur accélération pour un mouvement circulaire uniforme (vidéo) Pour un mouvement circulaire uniforme de rayon de
trajectoire R, le vecteur accélération et le vecteur vitesse d'un point mobile
sont :
L'accélération est centripète ( orientée vers le centre de la trajectoire).
Vitesse et accélération du centre d'inertie d'une planète, dans le
cas d'un mouvement circulaire uniforme En terminale, on considèrera que les orbites sont
circulaires. Dans le cas d'un mouvement circulaire uniforme les vecteurs
vitesse et accélération du centre d'inertie sont:
Démonstration prouvant que le mouvement est circulaire uniforme clique ici.
Dans le cas particulier du mouvement circulaire uniforme, la période de
révolution de la planète autour du soleil est :
Satellites de la terre en mouvement circulaire
uniforme Le mouvement des satellites se fait dans un plan
contenant le centre d'inertie de la terre GT. En effet la force 
de gravitation exercée par la terre sur le satellite est
centripète.
La vitesse et la période d'un satellite décrivant
une orbite circulaire à l’altitude h, centrée sur le centre d'inertie de
la Terre, sont :
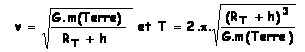
h: altitude du satellite(m); RT = 6400 km rayon de la terre. mT = 6.1024 kg
, masse de la terre.
G = 6,67.10-11 N.kg-2.m2 constante de
gravitation universelle.
Satellite géostationaire Un satellite est géostationnaire
s'il est toujours situé au-dessus du même point de la terre.
Il est immobile dans un
référentiel terrestre.
Comme son plan orbital doit contenir le centre de la terre, son orbite
est dans le plan de l'équateur. Sa période de révolution T est égale à la période
de rotation de la terre dans le référentiel géocentrique. Cette
période est appelée également jour sidéral. T
=23 h 56 min 4 s = 86164 s.
Chapitre 13 :
système mécanique oscillant, le pendule pesant
Le pendule pesant
Tout corps de masse 'm' effectuant des
oscillations autour d'un axe sous l'action de son poids est un pendule pesant.
Le pendule simple Un pendule simple est
constitué d'une masse 'm' qu'on considère entièrement concentrée au centre
d'inertie du pendule, et qui oscille autour d'un axe fixe. Lorsqu'un solide est écarté de la verticale, il est
animé d'un mouvement circulaire non uniforme, Il effectue des oscillations autour d'une position
équilibre verticale. C'est un système mécanique oscillant ou oscillateur
mécanique.
L'oscillateur mécanique Tout système mécanique
qui effectue un mouvement de va-et-vient de part et d'autre d'une position
d'équilibre est appelé oscillateur mécanique. Une oscillation est un aller-retour autour de la
position équilibre. Lorsque les oscillations se reproduisent à intervalle de temps fixe
l'oscillateur mécanique est alors dit périodique.
La période T d'un phénomène périodique est la plus petite durée au bout
de laquelle ce phénomène se reproduit identique à lui-même.
Unité : la seconde (s).
La fréquence f d'un oscillateur périodique correspond au nombre
d'oscillations effectuées par seconde. La fréquence est l'inverse de la période
:
unité : le Hertz (Hz)
Accélération du pendule (vidéo)Le vecteur accélération du centre d'inertie de la
masse est, d'après la seconde loi de Newton :
Détermination graphique d’un vecteur accélération clique ici.
Isochronisme des petites oscillations Pour des oscillations de faible amplitude la période ne dépend pas de
l'amplitude. On nomme ce phénomène l'isochronisme des petites
oscillations, les oscillations sont dites isochrones. Pour voir la vidéo de
l’expérience terrifiante clique ici. En l'absence de frottement on nomme période propre
To, la période des petites oscillations.
Expression de la période propre en fonction des paramètres du
pendule simple
La période propre du pendule simple attaché un fil de longueur 'l' dans un
champ de pesanteur d'intensité 'g' est :
Avec l(m) : longueur du fil ; g(m.s-2)
intensité du champ de pesanteur terrestre. Attention
cette expression n'est exacte que dans le cas des petites oscillations.
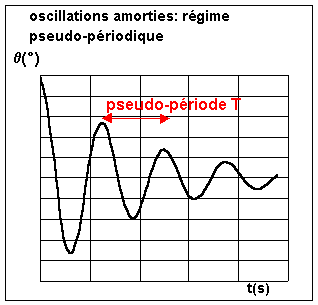
Pendule pesant amorti Le régime pseudo- périodique Pour un amortissement faible, l'amplitude diminue à
chaque aller-retour. Les oscillations du pendule sont amorties. On parle de
régime pseudo périodique, de pseudo période T» To Le
phénomène n'est pas périodique car il ne se répète pas identique à lui-même au
cours du temps (l'amplitude 
m diminue).
Le régime apériodique En augmentant encore les
frottements le pendule revient à sa position d'équilibre sans oscillations : le
mouvement est alors apériodique. Le pendule revient à sa position initiale sans
oscillation
Chapitre 14 : oscillateur mécanique
horizontal, système ressort masse
I) Force de rappel exercée par un ressort Soit un ressort de longueur à vide lo.
On modifie sa longueur en exerçant une force de tension à son extrémité libre,
en le comprimant ou l'étirant. La nouvelle longueur du ressort est notée 'l'. L'allongement 'a' du ressort est alors: a = l - lo.
Quand on comprime ou étire un ressort, celui
ci exerce une force de rappel sur
l'opérateur, proportionnelle à son allongement. Le coefficient de proportionnalité est appelé la
raideur 'k' du ressort. En orientant l'axe dans le sens de l'élongation du
ressort l'expression vectorielle de la force de rappel est:
F, valeur de la force de rappel en Newton (N); l longueur et lo longueur au repos du ressort en mètre(m); 
: vecteur unitaire orienté dans le sens de l'élongation ;k : raideur du ressort (N.m-1) ;
Oscillations libres non
amorties
On considère un solide de masse 'm' relié à un
ressort dont une des extrémités est fixe se déplaçant sur un plan horizontal
sans frottement :
L'origine O du repère est placée au point Go
position du centre d'inertie de la masse quand le ressort est au repos. Par
conséquent 
l'abscisse 'x' du point G, quand le ressort est étiré d'une longueur l,
est : x = l - lo.
Somme des forces extérieures appliquées à la masse 'm' :
Le plan est sans frottement donc la réaction est normale au plan. Elle
compense le poids par conséquent (vidéo):
Equation différentielle du mouvement (vidéo): La seconde loi de Newton ou principe fondamental de
la dynamique dit que la somme des forces extérieures agissant sur le solide est
égale au produit de la masse 'm' du solide par l'accélération de son centre
d'inertie G (d'abscisse 'x').
Par conséquent l'équation différentielle du mouvement d'un solide de
masse 'm’, soumis à une force de rappel d'un ressort de raideur k, sur un
plan horizontal sans frottement est (pour voir la démonstration
Solution de l'équation
différentielle
(vidéo)
On démontre que la solution de cette équation
différentielle est de la forme :
Avec : To(s), période propre de l'oscillateur (s); xm(m),
amplitude des oscillations ; 
(rad), phase à l'origine des dates. (vidéo).
Le solide effectue des
oscillations mécaniques libres sinusoïdales.
La période propre To (vidéo)
d'un oscillateur élastique en translation est : 
; m : masse du solide (kg)
;k : raideur du ressort (N.m-1).
Oscillations libres amorties On
distingue 2 régimes d'oscillations suivant l'importance des frottements : le régime pseudo périodique et le régime apériodique. (expérience).
Régime apériodique Le plan sur lequel se
déplace le solide relié au ressort, exerce une force de frottement. On étire le
ressort d'une longueur x = l - lo.
Lorsque les
frottements sont très importants le système mécanique {ressort, solide}
revient sans osciller à sa position initiale. Ce régime est appelé régime apériodique.
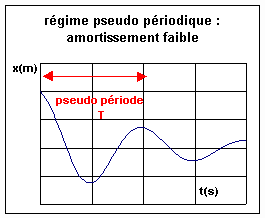
Régime pseudo-périodique Lorsque les frottements sont faibles, le système mécanique est le siège d'oscillations amorties d'allure sinusoïdale. Le phénomène ne se répète pas identique à lui-même,
on parle de phénomène pseudo périodique. La
pseudo période T est peu différente de la période propre d'oscillation libre
non amortie ( en faite elle est légèrement supérieure).
Le phénomène de résonance (expérience)Lorsqu'un excitateur impose des oscillations forcées
à un oscillateur, celui ci entre en résonance pour une période T proche de sa
période propre To. Son amplitude xm est
alors maximale. Ce phénomène est appelé la
résonance.
Si T (excitateur)» To alors xm= xm(max).