Chapitre 13 : système mécanique oscillant, le pendule pesant

Compétences exigibles au bac 3.1. Présentation de divers systèmes oscillants mécaniques Définir un pendule simple. Justifier la position d'équilibre dans le cas d'un pendule simple.) Définir l'écart à l'équilibre, l'abscisse angulaire, l'amplitude, la pseudo-période, la période propre et les mesurer sur un enregistrement. Enoncer la loi d'isochronisme des petites oscillations. Savoir comment un système peut atteindre un régime apériodique. Savoir que dans le cas d'un amortissement faible, la pseudo-période est voisine de la période propre. Pour un pendule simple, justifier la forme de l'expression de la période propre par analyse dimensionnelle. A partir d'une série de résultats expérimentaux, vérifier la validité de l'expression de la période propre d'un pendule simple. Savoir-faire expérimentaux Décrire un protocole expérimental permettant: - d'enregistrer le mouvement d'un système oscillant plus ou moins amorti - de vérifier la loi d'isochronisme des petites oscillations - de vérifier l'expression de la période propre dans le cas d'un pendule simple. 3.2 Le phénomène de résonance Savoir que la résonance mécanique se produit lorsque la période de l'excitateur est voisine de la période propre du résonateur. Savoir que l'augmentation de l'amortissement provoque une diminution de l'amplitude. Connaître des exemples de résonance mécanique Le pendule pesant Tout corps de masse 'm' effectuant des oscillations autour d'un axe sous l'action de son poids est un pendule pesant. Le pendule simpleUn pendule simple est constitué d'une masse 'm' qu'on considère entièrement concentrée au centre d'inertie du pendule, et qui oscille autour d'un axe fixe. Lorsqu'un solide est écarté de la verticale, il est animé d'un mouvement circulaire non uniforme,  Il effectue des oscillations autour d'une position équilibre verticale. C'est un système mécanique oscillant ou oscillateur mécanique. L'oscillateur mécanique Tout système mécanique qui effectue un mouvement de va-et-vient de part et d'autre d'une position d'équilibre est appelé oscillateur mécanique. Une oscillation est un aller-retour autour de la position équilibre. Oscillateur mécanique périodique Lorsque les oscillations se reproduisent à intervalle de temps fixe l'oscillateur mécanique est alors dit périodique. La période T d'un phénomène périodique est la plus petite durée au bout de laquelle ce phénomène se reproduit identique à lui-même. Unité : la seconde (s). La fréquence f d'un oscillateur périodique correspond au nombre d'oscillations effectuées par seconde. La fréquence est l'inverse de la période :

unité : le Hertz (Hz) Mouvement oscillatoire d'un pendule simple non amorti Accélération du pendule (vidéo) . Le vecteur accélération du centre d'inertie de la masse est, d'après la seconde loi de Newton : Détermination graphique d’un vecteur accélération (vidéo). Isochronisme des petites oscillations  Pour des oscillations de faible amplitude la période ne dépend pas de l'amplitude. On nomme ce phénomène l'isochronisme des petites oscillations, les oscillations sont dites isochrones (vidéo). En l'absence de frottement on nomme période propre To, la période des petites oscillations. période propre du pendule simple attaché un fil de longueur 'l' dans un champ de pesanteur d'intensité 'g' est : Avec l(m) : longueur du fil ; g(m.s^-2) intensité du champ de pesanteur terrestre. 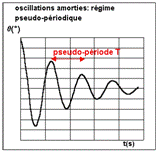Pendule pesant amorti régime pseudo- périodique Pour un amortissement faible, l'amplitude diminue à chaque aller-retour. Les oscillations du pendule sont amorties. 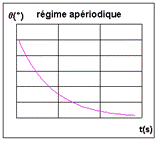On parle de régime pseudo périodique, de pseudo période T» To  Le phénomène n'est pas périodique car il ne se répète pas identique à lui-même au cours du temps (l'amplitude m diminue). Plus l'amortissement est important plus la décroissance des oscillations est importante. De plus, la pseudo période T augmente légèrement. Le régime apériodique En augmentant encore les frottements le pendule revient à sa position d'équilibre sans oscillations : le mouvement est alors apériodique. Le pendule revient à sa position initiale sans oscillation.