Chapitre 16 : le monde quantique

Compétences exigibles au bac L'atome et la mécanique de Newton: ouverture au monde quantique Connaître les expressions de la force d'interaction gravitationnelle et de la force d'interaction électrostatique. Savoir que l'énergie de l'atome est quantifiée et que la mécanique de Newton ne permet pas d'interpréter cette quantification. Connaître et exploiter la relation , connaître la signification de chaque terme et leur unité. Convertir les joules en eV et réciproquement. Interpréter un spectre de raies Dans les échanges d'énergie, associer le MeV au noyau et l'eV au cortège électronique Energie d'un photon  La lumière est constituée de corpuscules appelés photons.  A chaque photon correspond une onde électromagnétique de longueur d'onde ' l', de fréquence 'u ' et de célérité 'c' dans le vide (c=300 000 km.s^-1). Un photon a une masse nulle et une énergie E, produit de la constante de Planck 'h' par sa fréquence 'u '.  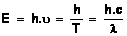Dans le cas ou le photon se déplace  dans le vide son énergie est : avec h = 6,62.10^-34J.s, T période de l'onde électromagnétique(s); 'u ' fréquence (Hz) ; 'c' célérité (m.s^-1). 1 eV = 1,6x10^-19 J Niveaux d'énergies quantifiées d'un atome : postulat de Bohr Afin d'interpréter le spectre d'émission de l'atome d'hydrogène, en 1913 M. Bohr énonce les postulats suivants : -L'atome possède différents niveaux d'énergie  bien définis, E1, E2, E3 etc. Il s'agit de valeurs discontinues (ou discrètes), et non de valeur continues. - Les variations d'énergie DE de l'atome sont quantifiées. - Quand l'atome passe d'un état d'énergie 'Ep' élevé à un niveau d'énergie 'En' plus faible il libère une énergie égale à  Ep - En.  - Le niveau de plus basse énergie de l'atome est appelée le niveau fondamental. Lorsqu'un atome se trouve à un niveau d'énergie supérieur au niveau fondamental, on dit qu'il est excité. Emission d'un photon au cours de la désexcitation Lorsqu'un atome se désexcite en effectuant une transition électronique d'un niveau d'énergie Ep à un niveau d'énergie plus faible 'En', il émet un photon d'énergie : Ep et  En en joule (J), h constante de Planck, h = 6,62.10^-34J.s , u fréquence(Hz) de l'onde électromagnétique associé au photon, c   (m.s^-1 ) célérité du photon. Interprétation énergétique des spectres atomiques Un gaz excité sous basse pressionémet, en se désexcitant, des rayonnements visibles (ou des rayonnements ultraviolets) possédant chacun une longueur d'onde. La valeur de l est déterminée par le passage d'un niveau d'énergie Ep supérieur à un niveau de plus basse énergie En :

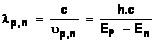
L'ensemble des rayonnements lumineux de longueur d'onde ln,p va produire le spectre de raies d'émission du gaz. Niveaux d'énergie électroniques d'un atome  Un atome peut acquérir différents niveaux d'énergie électronique qui proviennent de : * l'interaction des électrons entre eux et des électrons avec le noyau. * l'énergie cinétique des électrons. Lorsqu'un atome perd une partie de cette énergie en passant d'un niveau 'p' à un niveau 'n' il émet des rayonnements d'énergie de l'ordre de l'électron volt. Ces rayonnements se situent généralement dans le domaine du visible (400 nm < l < 800 nm) ou dans l'ultraviolet 10^-10m < l < 0,4.10^-6m Niveaux d'énergie d'un noyau Le noyau possède des niveaux d'énergie nucléaire du fait de l'interaction des nucléons. Les énergies correspondantes sont de l’ordre du MeV. Lors d'une désintégration radioactive le noyau fils Y est, en général, dans un état excité ( noté Y^* ). En se désexcitant, il émet un rayonnement g de forte énergie. La longueur d'onde l du rayonnement est de l'ordre du picomètre Niveaux d'énergie d'une molécule On distingue quatre types d'énergie au sein d'une molécule : Ee, énergie électronique des électrons. Comme pour les rayonnements électroniques des atomes, les rayonnements émis se trouvent dans le domaine du visible et des UV.  Et , énergie de translation de la molécule Ev , l'énergie de vibration due aux oscillations des noyaux autour de leur position d'équilibre.  La transition entre deux niveaux d'énergie de vibrations correspond à :  DE(vibration) = 0,1 eV Les longueurs d'onde correspondant à ce type de transition sont dans le domaine de l'infrarouge. Er ,l'énergie de la molécule autour de son centre d'inertie.  La transition entre deux niveaux d'énergie de rotation est de l'ordre du milli électronvolt. Les longueurs d'ondes correspondantes, font partie de l'infrarouge lointain.