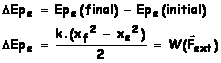Chapitre 15 : énergie mécanique

Connaissances exigibles au bac 4. Aspects énergétiques Connaître l'expression du travail élémentaire d'une force. établir l'expression du travail d'une force extérieure appliquée à l'extrémité d'un ressort, par méthode graphique et par intégration. établir et connaître l'expression de l'énergie potentielle élastique d'un ressort. établir l'expression de l'énergie mécanique d'un système solide-ressort et d'un projectile dans un champ de pesanteur. Exploiter la relation traduisant, lorsqu'elle est justifiée, la conservation de l'énergie mécanique du système. Calculer la variation de l'énergie cinétique d'un système à partir de la variation d'énergie potentielle et réciproquement. Savoir exploiter un document expérimental pour -calculer des énergies -reconnaître et interpréter la conservation ou la non-conservation de l'énergie mécanique d'un système. Travail d'une force constante Soit une force constante de norme F , appliquée entre les points A et B. Le travail de cette force entre le point A et B,  est égal au produit scalaire du vecteur déplacement par le vecteur force : WAB en joule (J), F en Newton(N), AB en mètre (m). (exemple vidéo : cas du pendule) Travail élémentaire d'une force variable On considère une force variable au cours du chemin AB. On découpe ce chemin en portions élémentaires de norme dli .On considère que la force de norme Fi qui s'applique le long de ce chemin élémentaire est constante.  Le travail élémentaire dWi de la force Fi le long du chemin élémentaire est : Pour déterminer la valeur totale du travail le long du chemin AB il faut faire la somme des travaux élémentaires dWi.  Cette somme est déterminée par un calcul intégral. Le travail d'une force non constante le long d'un chemin AB est égale à l'intégrale du produit scalaire du vecteur force, par le vecteur déplacement élémentaire : Travail d'une force exercée à l'extrémité d'un ressort On considère que l'extrémité libre du ressort est en équilibre tout au long du chemin, sous l'action de 2 forces : celle exercée par l'opérateur ( F ) et la force de rappel du ressort ( F' ). Par conséquent la force exercée par l'opérateur est opposée à la force de rappel du ressort  : Le travail d'une force appliquée à l'extrémité du ressort d'une position initiale xi à une position finale xf est : W en joule (J), x en mètre(m), k en Newton par mètre (N.m^-1).

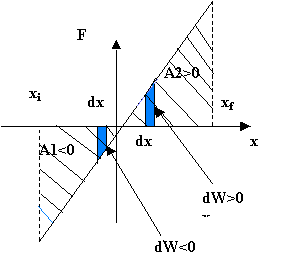
Détermination graphique du travail En représentant la coordonnée de la force exercée par l'opérateur en fonction de l'allongement x, on détermine graphiquement son travail. Sur le graphique représentant F = f(x), le travail de la force, exercée par le ressort, correspond à l'aire algébrique A = A1 + A2. Energie potentielle élastique d'un ressort Lorsqu'un ressort possède une élongation x, il emmagasine une énergie potentielle élastique.  L'énergie potentielle élastique, d'un ressort de raideur k, soumis à une élongation 'x' est : Epe (J), k (N.m^-1), x(m). Par convention à une élongation x = 0 correspond une énergie potentielle nulle (vidéo) Variation d'énergie potentielle élastique. Sous l'action du travail d'une force extérieure, l'élongation du ressort varie de xi à  xf . La variation d'énergie potentielle est égale au travail de la force extérieure. Energie mécanique du système solide-ressort L'énergie mécanique Em du système {masse, ressort} est égale à la somme de l'énergie potentielle élastique Epe, de l'énergie potentielle de pesanteur Epp, et de l'énergie cinétique Ec. L'énergie potentielle est nulle du fait du niveau zo de référence d'altitude choisie ( Epp = m.g.(z-zo)= 0 car z = zo). Dans le cas d'oscillations libres sans frottement, cette énergie mécanique est constante au cours du temps. Elle est égale à : Em en joule(J), k raideur du ressort (N.m^-1), xm amplitude des oscillations (m), 'm' masse du solide (kg), x(t) élongation du solide (m), v(t) vitesse du solide (m.s^-1). Quand x = xm , Epe(max) = Em = 1/2.k.xm^2et Ec = 0. Quand x = 0 Þ Epe = 0,  Em = Ec(max) = 1/2.m.v ^2(max) (vidéo) Oscillation libre avec frottement Lorsqu'on augmente les frottements, l'énergie mécanique diminue au cours du temps. Une partie est dissipée sous forme de chaleur. L'énergie mécanique totale diminue , elle est toujours en chaque instant égale à :  Em(t) = Epe(t)+Ec(t). Projectile dans un champ de pesanteur : cas de la chute libre Soit un solide de masse m, animé d'une vitesse v, situé à une altitude z, dans un champ de pesanteur d'intensité g. L'altitude de référence est notée zo . Il effectue un mouvement sans frottement à accélération constante. Il n’est donc soumis qu’à une seule force, son poids ! Il est animé d'une vitesse initiale vi et d'une altitude initiale zi. Son énergie mécanique se conserve. Elle est égale à la somme de son énergie cinétique et potentielle de pesanteur en chaque instant ( et donc à l'instant initial !) : Em, Epp, Ec en joule(J), m(kg), z et zo (m) , v(m.s^-1). Mouvement avec frottement Dans le cas d'un mouvement s'effectuant avec frottement, l'énergie mécanique diminue. Une partie de cette énergie est dissipée sous forme de chaleur. Considérons un mouvement dans un champ de pesanteur avec frottement. La variation d'énergie mécanique est égale au travail des forces de frottement :