Chapitre 6 : onde stationnaire

I) réflexion d'une onde sur un obstacle fixe

1)réflexion d'une onde progressive

Une onde incidente transversale se propage le long d'une corde et arrive sur un obstacle fixe. Elle se réfléchit avec une forme semblable mais inversé. La vitesse n'est pas modifiée, seul le sens de propagation est inversé.

2) vibrations d'un point du milieu de propagation

expérience : on utilise une onde progressive sinusoïdale envoyée le long d'une corde. Elle se réfléchit sur un obstacle fixe. On observe un point A de la corde.

L'élongation de ce point à l'instant 't'noté y(t) est la somme de l'élongation de l'onde incidente notée y₁(t) et de l'onde réfléchie notée y₂(t).:

___________________________y(t)= y₁(t) + y₂(t)

remarque :

Si l'onde incidente et réfléchie sont en opposition de phase au point A alors son élongation y(t)est____________ nulle quel que soit l'instant 't'.

On observe alors un ______________________nœud d'amplitude au point A.

Si en chaque instant y₁(t)=-y₂(t) alors y(t)=______0

Au contraire si l'onde incidente et réfléchie sont en phase alors le point A est le siège d'un ventre d'amplitude. Son amplitude ____________________est maximale.

Si y₁(t)=y₂(t) alors y(t)=____________2y₁(t)

II) onde stationnaire

rappel : la longueur d'onde est la distance parcourue par l'onde en une période.

l=_______________

v.T

v: vitesse de propagation de l'onde dans le milieu considéré(m/s)

T: période de vibrations de l'onde(s).

Chaque point de la corde vibre transversalement à une fréquence identique à celle de l'excitateur.

1)) production d'une onde stationnaires

activité 3 p56

Sur une corde on utilise une onde _____________ ____________ ________mécanique progressive sinusoïdale entretenue par un vibreur.

Pour une fréquence particulière f1 appelé ____________________________fréquence fondamentale ou premier harmonique, on observe _________ _______________________

des ondes stationnaires.

On observe également des ondes stationnaires pour un nombre _____________ ___________ _____________________.

n entier de la fréquence fondamentale.

2)Définition

Une onde sur une corde est stationnaire, quand on n'observe plus de propagation longitudinale mais uniquement un déplacement transversal de chacun de ses points.

Les points Qui ne vibrent pas sont appelés des nœuds d'amplitude en ces points les amplitudes des ondes incidentes et réfléchies s'annulent (elles sont en opposition de phase).

Les points qui vibrent avec une amplitude maximale sont appelés des ventres d'amplitude. En ces points les amplitudes des ondes incidentes et réfléchis s'ajoutent (elles sont en phase).

3) condition nécessaire pour obtenir une onde stationnaire

Pour obtenir une onde stationnaire toutes les ondes qui se propagent dans le même sens doivent arriver________ _____________________________ ______________.

en phase au point A considéré. La première onde arrive à l'instant t1. Elle effectue ensuite un aller-retour (avec deux réflexions sur les deux extrémités fixes de la corde) et revient à l'instant t2 au point A:

Dt=t2-t1=2L/v

Si Dt=n.T par exemple alors l'onde 1 et l'onde 2 seront en phase en effet leur équation est du type:

y1=Y1 cos[(2.P/T).t] et

y2=Y2.cos [(2.P/T).t+n.T]=

Y2.cos[(2.P/T).t]

pour que deux ondes consécutives soient en phase et qu'on obtienne des ondes stationnaires il faut que la condition suivante soit vérifiée :

Dt=n.T avec n entier, et T période de vibrations de l'onde.

Par conséquent :

n.T=2.L/v soit L=n.l/2

Pourquoi a-t-on des nœuds d'amplitude ?

Toutes les ondes se déplaçant de droite à gauche arrive au point A en phase. Par contre toutes celles arrivent de gauche à droite arrive en opposition de phase avec ces dernières. Par conséquent les amplitudes s'annulent on obtient un noeud d'amplitude.

Pourquoi obtient-on des ventres d'amplitude ?

Les ondes se déplaçant de gauche à droite arrive en phase avec les ondes se déplaçant de droite à gauche toutes les amplitudes s'ajoutent : on obtient un ventre d'amplitude.

4) relation entre tension de la corde et longueur L dans le cas des ondes stationnaires

Rappel: la vitesse de propagation le long d'une corde est :

v=(F/m)^1/2

F: tension de la corde (N)

m: masse linéique de la corde

par conséquent dans le cas des ondes stationnaires :

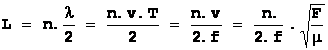
on obtient des ondes stationnaires pour les fréquences correspondantes aux modes propres de vibrations :

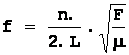
Pour n=1 on retrouve la fréquence du fondamental. Pour n=2 la fréquence du second harmonique, etc.

III) onde stationnaire dans une colonned'air

activité 5 page 59

1) dispositif expérimental

voir chapitre précédent

2) interprétation

Aux deux extrémités ouvertes du tube on détecte des _____________________

ventres d'amplitude des couches d'air donc des _____________ _____________________noeuds de pression.

Ces nœuds de pression correspondent au noeuds d'amplitude dans le cas une corde.

À l'intérieur du tube. On détecte des noeuds d'amplitude donc des ventres de pression. Ces ventre de pression correspondent au __________ ___________________ventre d'amplitude pour la corde.

Deux nœuds ou de ventres de pression consécutifs sont séparés d'une distance l/2.

La longueur L du tuyau correspond à un nombre entier n de demi longueur d'ondes .

L=_____________ ______________

v: vitesse de propagation des sons dans l'air(environ 340m/S)

n.l/2=n.v.T/2=n.v/(2f)

Les fréquences propres correspondantes aux modes propres de vibration sont:

f= _________________

Remarque: pour des fréquences différentes des fréquences propres on n'observe pas d'ondes stationnaires.