Résistance d’une bobine réelle (Polynésie 2006 6 points ) énoncé

A. Résistance d’une bobine réelle

1) Vidéo

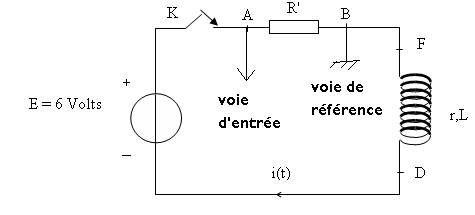
L’ampèremètre est placé en série .Le courant entre par la borne A et sort par la borne COM. Le voltmètre est placé en dérivation. Sa borne COM est relié au point D, on mesure la tension

Ub = U_FD

Remarque : si on relie la borne COM à la borne F on mesure la tension U_DF

2) La tension aux bornes de la bobine vaut :

en régime permanent l’intensité i = constante = I_b

Par conséquent di/dt = 0 donc ub = U_b = r₁ I_b

B – En régime transitoire

1) La bobine s’oppose à l’établissement du courant. On observe un régime transitoire pendant lequel l’intensité du courant augmente, puis un régime permanant avec

i = I_b = constante

2)

La tension lue par le système d’acquisition vaut d’après loi d’ohm :

u_AB(t) = R’.i(t)

u_AB est proportionnelle à i. Le coefficient de proportionnalité est R’

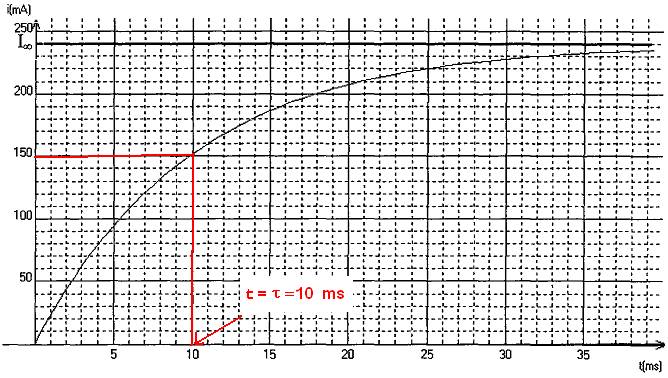3) On sait que :

avec i_max = 240 mA = 0,240 A donc

D’après le graphe la figure ci dessous, on repère le point d’ordonnée 150 mA. Celui ci à pour abscisse :

4.1 dans cet exercice : Pour voir la correction clique ici.

4.2 Calcul de r₂

5.1 D’après la loi d’additivité des tensions :

E = u_b + u_R’ = u_b = r₃.i + L. di/dt + u_R’

En régime permanent i = constante = donc

E = U_b + U_R’ = r. I_¥ + R’. I_¥

r. I_¥ = E – R’. I_¥

6.1

les valeurs sont cohérentes entre elles.

C – En régime oscillatoire

1.1 La période propre d’un oscillateur ( circuit LC sans résistance dans le circuit) vaut :

1.2 T₀. = = 6 x 10^-3 s

2.1 Au cours du temps de l’énergie est dissipée par effet joule à travers la résistance. L’amplitude des oscillations diminue.

2.2 Vidéo

base de temps : 2x10^-3 s/div ; nombre de division compris entre 6,2 et 6,4.

6,2x 2x10^-3 s < 2T < 6,4x 2x10^-3 s

6,2x10^-3 s < T < 6,4x10^-3 s

2.3 Les valeurs extrêmes obtenues pour la pseudo période sont peu différentes de To = 6 x 10^-3 s