Réponse d'une bobine à un échelon de tension énoncé
Q1
D'après la loi d'additivité des tensions :
E
= R'.i + Ldi/dt + r.i
or en régime permanent le courant ne varie plus donc :
ce qui donne l'expression précédente simplifiée.(on remplace i par I qui correspond à l’intensité du
courant en régime permanent):
E = R'.I + r.I = (R'+r).I
Les malins auront vu sur
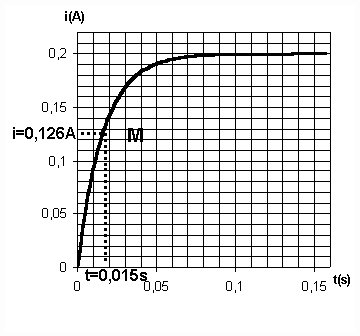
la courbe qu'en régime permanent i = i(max) = I = 0,2 A!
Q2
Donnée: i (t = 
) = 0,63.I = 0,63 x
0,2 = 0,126 A
Quand le courant atteint une valeur de 0,126 A environ la durée écoulée
est t = .
Allez, on reprend la courbe! Le point M(t = = 0,015 s , i = 0,126
A) nous donne la valeur de la constante de circuit, avec une précision faible
vue la taille de la courbe.
Le dicton du jour: Pâturage nouveau réjouit le veau !
Q3
A t = ,
i = 0,63.I = 0,126 A.
On reprend la technique vue dans la question Q2 : l'abscisse du point M
d'ordonnée i = 0,126 A à pour abscisse t = .
La détermination graphique nous donne les différentes valeurs de :
|
L(H) |
0,20 |
0,4 |
0,6 |
0,8 |
|
t (ms) |
4 |
8 |
12 |
16 |
La valeur de pour L = 0,8 H peut
être déterminée avec une plus grande précision que dans la question Q2 ( t » 15
ms) du fait de la plus grande précision de la courbe.
Q4
a) Il paraît évident qu'il existe une relation de proportionnalité entre
L et t, on reprend le tableau
précédent et on calcule le rapport L/t . On trouve la valeur 50
donc :
L = 50 x
On peut, si les valeurs L/ sont légèrement
différentes les unes des autres, en faire la moyenne. On aurait pu également
tracer la courbe représentative de la fonction L= f( ) et trouver le
coefficient directeur qui vaut 50! ( bon j'arrête!) .
|
L(H) |
0.20 |
0.4 |
0.6 |
0.8 |
|
|
4.10-3 |
810-3 |
1210-3 |
1610-3 |
|
L/ |
50 |
50 |
50 |
50 |
b) Cette valeur est parfaitement en accord avec la valeur R = 50 W donnée dans l'énoncé! Bravo. Il est temps d'aller dormir,
il se fait tard, il faut que j'aille chercher ma mémé demain au train très tôt.
Q5
a) Pour voir la vidéo clique
ici.
b) A la date t = 0 s la tension s'écrit :
E = L[ di/dt ] t = 0 + R.i(0)
or i(0) = O A donc E = L[di/dt] t=0
Juste après la fermeture de l'interrupteur, la tension aux bornes d'une
bobine est égale à E.
Avant la fermeture de l'interrupteur la tension aux bornes de la bobine
est nulle (la bobine est un dipôle passif).
U(bobine)avant fermeture de l'interrupteur = 0
Par conséquent il n'y a pas continuité de la valeur
de la tension aux bornes d'une bobine.
Remarque : l'intensité aux bornes d’une bobine est continue, puisque
la bobine s'oppose à toute variation brutale du courant dans le circuit.
Q6
a) D'après la question Q5 à t = O s, i = 0 A donc :
donc :
Or di/dt (dérivée de l'intensité du courant par
rapport au temps) est égale à la pente
de la tangente à l'instant considéré.
En t = 0 s la tangente est une droite qui passe par l'origine
d'équation i = a.t avec:
donc :
L'équation de la tangente à t = 0
est:
Pour t = 
on a:
b) La tangente à la courbe en t = O s coupe
l'asymptote horizontale i = I en un point M d'abscisse
t = !
Le proverbe du jour: "les autres sont le miroir de ton âme" à
méditer …….