Sonde thermique (bac Antilles 2005 ) énoncé

Q1

a) Vidéo

D’après la loi d'additivité des tensions :

E = u_R + u_C

b). Vidéo

Equation différentielle en u_C :

i = dq/dt; u_R = R.i ; u_C =q/C implique:

Q2

a) u_C = A + B.exp(-t/t) (1)

t ® +¥ , -t/t ® -¥

B.exp(-t/t) ® 0

u_C ® A

Or lorsque ‘t’ tend vers l’infini le condensateur est complètement chargé, sa tension est égale à celle du générateur :

u_C = E Þ A = E

b) A t = 0, u_C = 0 or e⁰ = 1 Þ

B.exp(-t/t) = B

D’après l’équation 1 :

0 = E + B Þ

B = -E

c) u_C = A + B.exp(-t/t) et A = E, B = - E

u_C = E –E. exp(-t/t) = E(1 - exp(-t/t) )

u_C = E(1 - exp(-t/t) )

Q3

a) Vidéo

b) A t = t₁ , u_C (t₁) = 0 ,63.u_C(max) Þ u_C (t₁) = 0,63 x 4 = 2,5V.

Graphiquement le point d’ordonnée 2,5 V à pour abscisse t = t₁ = 1,3 ms =1,3 x 10^-3 s

c) Calcul de R₁ (C = 1 mF = 10^{-6 F)}

t₁ = R₁.C Þ R₁ = t₁/C = (1,3 x 10^-3)/(10^-6) Þ

R₁ = 1,3 x 10³ W

Tableaux de résultats :

Température q (°C)	q1 = 20	25	30	35	40	45	50	55	60
Constante de temps t (ms)	t1 =1,3		0,9		0,6		0,4		0,3
Résistance R (kW) = t /C	R1 = 1,3	1,1	0,90	0,74	0,6	0,49	0,4	0,34	0,3

Q4

a)Tracé de la courbe :

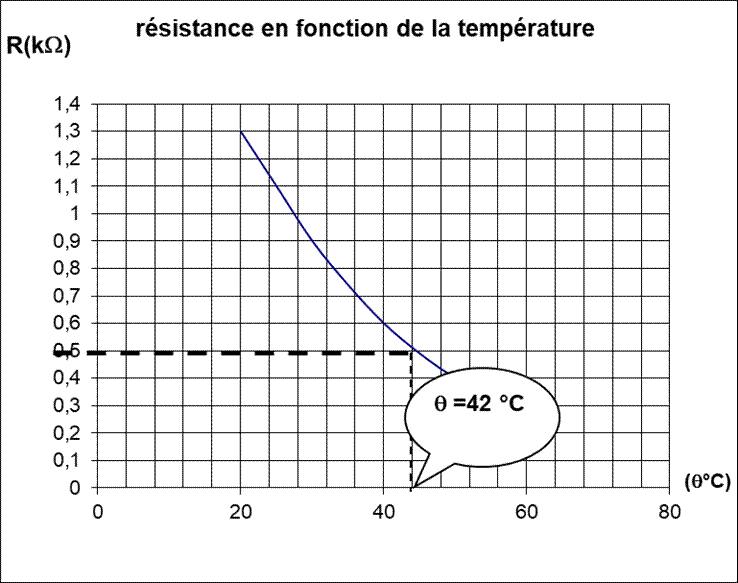
b) Le point, d’ordonnée R = 0,50 kW, a pour abscisse q = 42 °C.