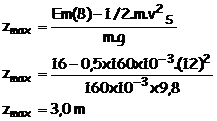LE HOCKEY SUR GAZON (Amérique du Nord 2009 5 points) énoncé

A – Première phase

1.1. (vidéo) Deuxième loi de Newton : Dans un référentiel galiléen, la somme des forces extérieures exercée sur un système de masse m est égale au produit de la masse m par le vecteur accélération  :

Etude mécanique :

système {balle}

référentiel terrestre supposé galiléen.

Le poids de la balle et l’action de l’air sont négligé devant la force exercée par la crosse, la deuxième loi de Newton appliquée à la balle le long du trajet AB s’écrit :

.

1.2. (vidéo) D’après la seconde loi de Newton le vecteur accélération est uniforme :

de plus La trajectoire de la balle entre A et B, est une droite : le mouvement est rectiligne uniformément accéléré.

2.1 (vidéo ) Par définition du vecteur accélération est égale à la dérivée du vecteur vitesse par rapport au temps :

.

2.2 (vidéo ) Comme le vecteur accélération est constant entre A et B il vient :

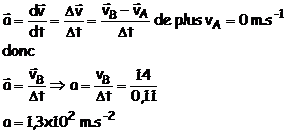
3.

F = m.a = 0,160 ´ 1,3´10²

F = 20 N.

Le poids de l’objet a pour valeur :

P = m.g = 0,160 ´ 9,8 = 1,6 N.

conclusion : la valeur de la force F est 13 fois plus grande que celle du poids de la balle. Une grandeur peut être négligées si elle est 100 fois inférieure à une autre donc P ne peut être négligé devant F

.

B – Deuxième phase

1. Trajectoire de la balle.

1.1. (vidéo)Le mouvement de la balle est étudié dans le référentiel terrestre associé au repère (O,x,z) .

Coordonnées du vecteur vitesse à l’instant t = 0 :

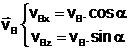
1.2. (vidéo)Coordonnées du vecteur position à l’instant t = 0

1.3. (vidéo)Coordonnées du vecteur vitesse au cours du temps :

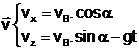
Au sommet S de la trajectoire, le vecteur vitesse de la balle à une direction horizontale  : v_Sz = 0.

par conséquent la valeur vs est :

v_S = v_B.cos = 14 ´ cos(30)

v_S = 12 m.s^-1.

1.4. (exemple d’exercice similaire)Le vecteur vitesse est la dérivée du vecteur position par rapport au temps par conséquent :

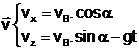
Les conditions initiales sont x(0) = x_B = 0 et z(0) = z_B = h . Par intégration on obtient les équations horaires des coordonnées du vecteur position :

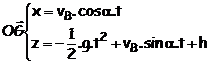
1.5. (vidéo) Équation de la trajectoire : c’est la relation liant x et z. On exprime le temps ‘t’ en fonction de x, puis on réinjecte cette valeur dans l’expression de z ::

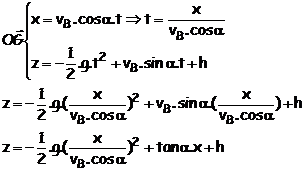
2.1. Pour que le but soit marqué il faut pour x = d, que 0 z(d) L(hauteur des cages). Il faut également que le palet ne roule pas après son contact avec le sol !!

2.2. On remplace la valeur x = d = 15 m dans l’équation de la trajectoire :

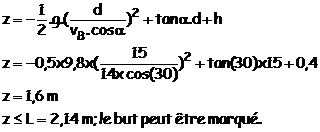
C – Étude énergétique 

1. Énergie potentielle de pesanteur : E_p(z) = m.g.z

Énergie mécanique : E_M = E_C + E_P = ½.m.v² + m.g.z

2. (vidéo)Au point B : E_M(B) = ½.m.v_B² + m.g.h = 0,5 ´ 0,160 ´ (14²) + 0,160 ´ 9,8 ´ 0,40 = 16 J.

3.1. Il n’y a pas de frottement donc l’énergie mécanique est constante au cours du mouvement de la balle.

3.2. (vidéo)D’après le 3.1

E_M(B) = E_M(S) = constante

E_M(B) = ½.m.v_S² + m.g.z_max

E_M (B)– ½.m.v_S² = m.g.z_max