Comment
se déplace un satellite sur son orbite ?
En première approximation, un satellite est pratiquement
soumis uniquement à une force centrale, la force de gravitation exercée par la Terre.
Son mouvement dans le référentiel géocentrique peut être prédit par les lois de la
mécanique, avec une mention toute particulière pour la relation suivante, où F
représente la force subie par le solide de masse m, et a son accélération :
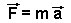
Dans le cas d'un objet soumis à une force centrale,
l'intégration de cette équation permet de montrer que la trajectoire est une conique
qui, pour des vitesses initiales pas trop grandes, est fermée : l'objet est satellisé,
il est en orbite autour de la Terre...
Conformément aux trois lois de Kepler :
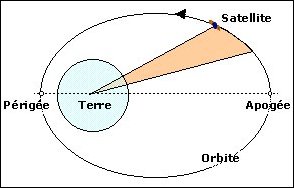
- La trajectoire est plane, c'est une ellipse dont le centre
de la Terre occupe l'un des foyers.
- L'aire balayée par le rayon vecteur Terre-Satellite en une
durée donnée est constante.
|
|
- Le rapport du carré de la période
orbitale au cube du demi grand axe de la trajectoire est constant.
T2 / a3 = constante
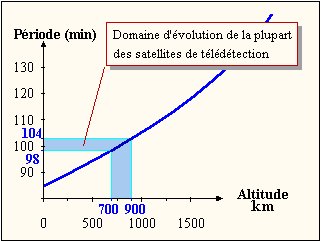
Dans le cas de satellites en orbite circulaire, la période
dépend donc uniquement du rayon de l'orbite.
Ci-contre : période des satellites en orbite basse en fonction de
l'altitude (d'après le cédérom "Les images satellitales").
|
 |
En conclusion...
Dans le référentiel géocentrique, la forme de la
trajectoire est simple et dépend uniquement des conditions initiales du mouvement. Pour
prévoir la position d'un satellite dans l'espace, il suffit donc de connaître les
paramètres relatifs :
- à la forme de la trajectoire,
- à la position de la trajectoire dans l'espace,
- à la position de la trajectoire dans son plan,
et de connaître la position du satellite à un instant
donné.
Dans le cas d'une trajectoire
circulaire, quatre paramètres sont nécessaires : trois pour déterminer la
trajectoire et un pour fixer la position initiale.
Dans le cas d'une trajectoire
elliptique, six paramètres sont nécessaires.
|