chapitre 9 : transformation forcées
DE L’IMPORTANCE DE L’EAU OXYGÉNÉE (Liban 2009 7 points) corrigé
Synthétisée pour la première fois en
1818 par le Baron Louis Jacques Thénard, l’eau
oxygénée ou peroxyde d’hydrogène H2O2
est d’une très grande utilité et d’une
grande importance économique. Elle est utilisée pour le
blanchiment de la pâte à papier et des textiles naturels ou
synthétiques, le désencrage des vieux papiers et le traitement
des eaux usées. C’est également un antiseptique
pharmaceutique et un agent de stérilisation en industrie alimentaire.L’eau
oxygénée peut être synthétisée à
partir du dihydrogène gazeux et du
dioxygène gazeux par une réaction dont l’équation
s’écrit : H2(g) + O2(g) = H2O2(l)
Les parties 1 et 2 sont indépendantes
1. Préparation du dihydrogène par électrolyse
Données :
Couples oxydant/réducteur : Cl2(g)/Cl –(aq) ; H+(aq)/H2(g)
Constante d’Avogadro : NA = 6,02.1023 mol-1
Charge électrique élémentaire : e = 1,60.10 – 19 C
Volume molaire dans les conditions de l’expérience : Vm = 30,0 L.mol-1
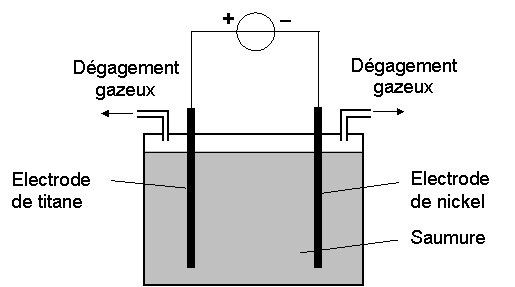
Le dihydrogène nécessaire à la synthèse de l’eau oxygénée doit être très pur. Il est obtenu par électrolyse d’une saumure, c'est-à-dire d’une solution aqueuse concentrée de chlorure de sodium (Na+(aq) + Cl –(aq)). Le schéma simplifié du dispositif est représenté en annexe à rendre avec la copie.
1.1. Identifier l’anode et la cathode sur le schéma de l’annexe à rendre avec la copie et indiquer le sens de déplacement des différents porteurs de charge.
1.2. On obtient un dégagement de dichlore à l’anode et de dihydrogène à la cathode. Écrire les demi-équations des réactions se produisant aux électrodes.
1.3. Montrer que pour une intensité du courant I et une durée de fonctionnement Dt données, le volume de dihydrogène produit à la cathode s’écrit :
![]()
1.4. L’intensité du courant vaut I = 5,00.104 A, calculer le volume de dihydrogène produit par heure de fonctionnement.
2. Cinétique de la dismutation de l’eau oxygénée
La solution aqueuse d’eau oxygénée se décompose lentement en dioxygène O2(g) et en eau selon la réaction d’équation : 2 H2O2(aq) = O2(g) + 2 H2O(l)
On veut effectuer le suivi cinétique de cette réaction, supposée totale, à la température de 25°C. La décomposition de l’eau oxygénée étant très lente, celle-ci doit être catalysée par les ions fer III (Fe3+).
À l’instant t = 0, on mélange :
·
V = 24 mL
de solution aqueuse d’eau oxygénée de concentration molaire
en
soluté apporté c = 2,5 mol.L-1
· 6,0 mL de solution aqueuse de chlorure de fer III (Fe3+(aq) + 3 Cl –(aq))
· de l’eau distillée jusqu’à obtenir une solution de volume total VT = 1,0 L
Un dispositif permet de recueillir et de mesurer le volume de dioxygène VO2 dégagé à la pression atmosphérique P = 1,013.105 Pa. Le volume total de la solution VT = 1,0 L est supposé rester constant au cours de l’expérience. Les résultats sont consignés dans le tableau suivant :
|
t (min) |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
60 |
|
|
0 |
160 |
270 |
360 |
440 |
500 |
540 |
590 |
610 |
680 |
On admet que dans les conditions de l’expérience, le dioxygène peut être considéré comme un gaz parfait. On rappelle la loi des gaz parfaits ; PV = nRT avec :
· P : pression du gaz en Pa
· V : volume du gaz en m3
· n : quantité de matière de gaz en mol
· R : constante des gaz parfaits ; sa valeur est égale à 8,31 J.mol-1.K-1
· T : température absolue exprimée en Kelvin (K) ; T est reliée à θ, température exprimée en degré Celsius (°C) par la relation : T = 273,15 + θ
2.1. Avancement de la réaction
2.1.1. Compléter le tableau d’avancement de la réaction représenté en annexe à rendre avec la copie.
2.1.2. Calculer la valeur de l’avancement maximal xmax de la réaction.
2.1.3. Établir l’expression de l’avancement x(t) de la réaction en fonction du volume de dioxygène VO2(t) formé.
2.1.4. Calculer sa valeur à l’instant t = 30 min.
2.2. Analyse du graphe x(t)
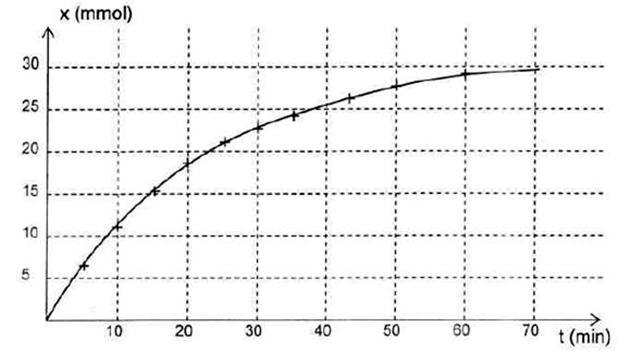
2.2.1. Le graphe représentant l’avancement x en fonction du temps t est fourni en annexe à rendre avec la copie. Définir le temps de demi-réaction t1/2 et déterminer sa valeur à partir d’une construction graphique.
2.2.2. Quelle information de graphe x(t) donne-t-il sur l’évolution de la vitesse de la réaction au cours du temps ? Justifier la réponse.
2.3. Facteurs cinétiques
2.3.1. Quel facteur cinétique permet d’expliquer l’évolution de la vitesse de la réaction au cours du temps ? Interpréter microscopiquement cette évolution.
2.3.2. Dessiner sur le graphe de l’annexe l’allure de la courbe que l’on aurait obtenue si l’expérience avait été réalisée à une température plus élevée. Justifier.
2.3.3. Dire, en justifiant, si les propositions suivantes sont VRAIES ou FAUSSES dans le cas où le même mélange initial est cette fois complété avec de l’eau distillée jusqu’à obtenir une solution de volume total V’T = 0,50 L :
· Proposition 1 : L’avancement final est divisé par deux.
· Proposition 2 : L’état final est atteint plus rapidement.
2.4. Importance du catalyseur
2.4.1. Rappeler la définition d’un catalyseur.
2.4.2. Lors de ce suivi cinétique, la catalyse mise en jeu est-elle homogène ou hétérogène ? Justifier.
Annexe à rendre avec la copie
 1. Préparation du
dihydrogène par électrolyse :
1. Préparation du
dihydrogène par électrolyse :
2. Cinétique de la dismutation de l’eau oxygénée :
Tableau d’avancement :
|
|
2 H2O2(aq) = O2(g) + 2 H2O(l) |
|||
|
État |
Avancement |
Quantités de matière en mol |
||
|
État initial |
|
|
|
Excès |
|
En cours de transformation |
|
|
|
Excès |
|
État final |
|
|
|
Excès |
Avancement x en fonction du temps t
 |