Chapitre 16 : le monde quantique /onde lumineuse

Lampe à vapeur de sodium (5,5 points 2007/09 Polynésie )

Corrigé

 

Lors d'une séance de travaux pratiques, des élèves utilisent une lampe à vapeur de sodium. Celle-ci émet une lumière jaune-orangé. Afin de comprendre l'origine de cette couleur, ils consultent leur livre de physique dans lequel figure le diagramme énergétique simplifié de l'atome de sodium reproduit ci-dessous :

 

Le niveau n = 1 est celui de plus basse énergie.

Données :

•         masse de l'électron : me = 9,10.10-31 kg

•         masse du proton :     mp = 1,67.10-27 kg

•         constante de gravitation universelle : G = 6,67.10-11 SI

•   charge électrique élémentaire : e = 1,60.10-19 C

•   constante de Planck : h = 6,63.10-34 J.s

•    célérité de la lumière dans le vide : c = 3.108 m.s-1.

1eV = 1,6x10-19 J

aide au calcul :

 

1. Étude de l'atome de sodium

1.1. Donner la composition de l'atome de sodium .

1.2.           Le diagramme énergétique simplifié de l'atome de sodium montre que l'énergie ne peut prendre que certaines valeurs. Comment qualifie-t-on alors l'énergie ? La mécanique de Newton permet-elle d'expliquer ces niveaux énergétiques ?

1.3.           La couleur jaune-orangé correspond à une transition concernant les deux premiers niveaux (n = 1 et n = 2). Représenter cette transition par une flèche sur le diagramme énergétique donné en annexe à rendre avec la copie dans le cas d'une émission. Calculer la longueur d'onde  de la radiation émise par la lampe.

1.4.           Déterminer, d'après le diagramme, la plus courte longueur d'onde de la radiation que peut émettre l'atome de sodium. On arrondira les données avec 1 chiffre significatif avant d’éffectuer . Préciser, en le justifiant, à quel domaine spectral appartient cette radiation.

 

2. Dispersion de la lumière émise

Afin d'étudier la radiation de couleur jaune-orangé, les élèves décident de l'isoler des autres radiations éventuellement émises par la lampe. Pour cela ils réalisent la dispersion de la lumière émise grâce à un prisme en verre.

2.1. 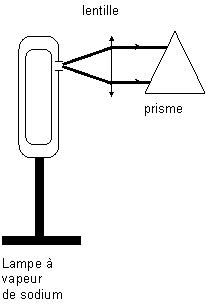             Le verre est un milieu dispersif, expliquer ce terme.

2.2.             La fréquence de la radiation jaune-orangé est-elle différente dans le verre et dans l'air ?

2.3.             À cette fréquence, l'indice de réfraction du verre pour la radiation jaune-orangé est n = 1,52. Après avoir défini l'indice d'un milieu transparent, calculer la valeur de la longueur d'onde  de la radiation jaune-orangé dans le verre.

2.4.             À la sortie du prisme, on sélectionne la radiation jaune-orangé de longueur d'onde. Comment qualifie-t-on une telle lumière ?

3.                 Diffraction de la lumière jaune-orangé

Les élèves décident d'utiliser le phénomène de diffraction pour vérifier la valeur de la longueur d'onde l de la radiation jaune-orangé. Pour cela ils disposent une fente fine verticale sur le trajet de la lumière.

3.1.           Les élèves ont à leur disposition trois fentes de largeur a différente. Quel doit être leur choix afin que le phénomène de diffraction soit le plus marqué possible ?

3.2.           Le phénomène de diffraction existe-t-il dans d'autres domaines que celui de la lumière ? Si oui, donner un exemple avec un schéma explicatif.

3.3.           Derrière la fente, à une distance D = 1,0 m, les élèves disposent un écran perpendiculairement à la direction de propagation de la lumière. Dessiner l'allure de ce qu'on observe sur l'écran sur l'annexe à rendre avec la copie.

3.4.           Dans la pratique, la figure de diffraction est peu lumineuse. La distance L, entre les deux extinctions de part et d'autre de la tache centrale, a néanmoins pu être mesurée à l'aide d'une lunette de visée. La valeur obtenue est L = 2,4 cm. Montrer que la longueur d'onde  peut s'exprimer par

3.5.           . Faire l'application numérique sachant que la fente a une largeur a = 50 µm.

 

ANNEXE À RENDRE AVEC LA COPIE

 

 

1.3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


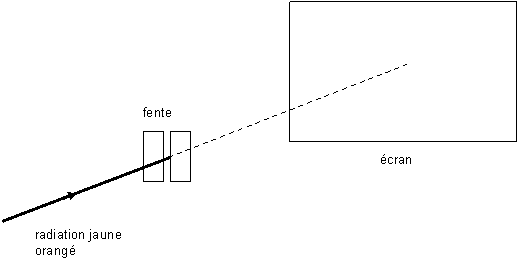
3.3