sciences physiques nouveau programme

Sommaire Terminale spécialité

Mouvements et interactions

12. Mouvement dans un champ uniforme / seconde loi de Newton

Cours / Activités expérimentales

Annales de bac /activités

Animations

Vidéos de cours

Cours :

Activités expérimentales

Fiches méthodes

Puissances de 10, notation scientifique

Unités légales du système international / conversion

Méthode de résolution d’exercices

Résoudre une équation à une inconnue

Programme officiel

Notions et contenus

Capacités exigibles

Activités expérimentales support de la formation

2. Relier les actions appliquées à un système à son mouvement

Deuxième loi de Newton

Centre de masse d’un système.

Justifier qualitativement la position du centre de masse d’un système, cette position étant donnée.

Référentiel galiléen.

Deuxième loi de Newton.

Équilibre d'un système.

Discuter qualitativement du caractère galiléen d’un référentiel donné pour le mouvement étudié.

Utiliser la deuxième loi de Newton dans des situations variées pour en déduire :

- le vecteur accélération du centre de masse, les forces appliquées au système étant connues ;

- la somme des forces appliquées au système, le mouvement du centre de masse étant connu.

Mouvement dans un champ uniforme

Mouvement dans un champ de pesanteur uniforme.

Champ électrique créé par un condensateur plan. Mouvement d’une particule chargée dans un champ électrique uniforme. .

Montrer que le mouvement dans un champ uniforme est plan.

Établir et exploiter les équations horaires du mouvement.

Établir l’équation de la trajectoire.

Discuter de l’influence des grandeurs physiques sur les caractéristiques du champ électrique créé par un condensateur plan, son expression étant donnée.

Principe de l’accélérateur linéaire de particules chargées.

Décrire le principe d’un accélérateur linéaire de particules chargées.

Aspect énergétiqueEx

ploiter la conservation de l’énergie mécanique ou le théorème de l’énergie cinétique dans le cas du mouvement dans un champ uniforme.

Utiliser des capteurs ou une vidéo pour déterminer les équations horaires du mouvement du centre de masse d’un système dans un champ uniforme. Étudier l’évolution des énergies cinétique, potentielle et mécanique.

Capacité numérique : Représenter, à partir de données expérimentales variées, l’évolution des grandeurs énergétiques d’un système en mouvement dans un champ uniforme à l’aide d’un langage de programmation ou d’un tableur.

Capacités mathématiques : Résoudre une équation différentielle, déterminer la primitive d’une fonction, utiliser la représentation paramétrique d’une courbe.

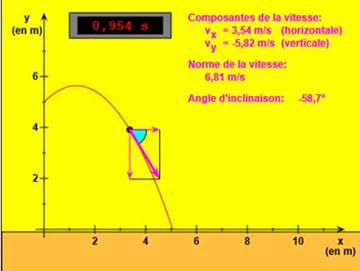
1. tournoi des 6 nations

mouvement parabolique; équations horaires du mouvement; équation de la trajectoire; calcul de la vitesse à un instant donné; portée de la trajectoire; poussée d'Archimède;

Corrigé

2. le saut de la grenouille (USA 2004)

détermination graphique de vitesse et d'accélération; seconde loi de Newton; équation horaire; sommet de la trajectoire; calcul de la vitesse initiale

Corrigé

3. lancer du poids au championnat du monde (Nouvelle Calédonie 2004)

courbe vx(t), vy(t): calcul de la vitesse initiale; vitesse au sommet de la trajectoire; rapport entre la poussée d'Archimède et le poids P; seconde loi de Newton; équation horaire du mouvement; équation de la trajectoire; condition sur l'angle et la vitesse initiale pour que la portée soit maximale;

Corrigé

4. Spectromètre de masse (Polynésie 2014, labolycée)

5. Les débuts de l’électron en physique (Labolycée)

6. Détermination du rapport e/m de l’électron (Labolycée)

7. Le jet d’eau de Genève (non corrigé EC, Labolycée, python)

8. L’exploit d’Alan Eustace (EC, Labolycée, python, champ de pesanteur)

9. Performance d’un cycliste (EC Labolycée, python, non corrigé)

10. Etude d’une montagne russe (EC Labolycée, python, énergie mécanique, tracé de vecteur vitesse, TEC)

11. Le rugby, sport de contact et d’évitement (Liban 2013)

Attention ne pas faire le 1.2 et 1.3 , hors programme

Corrigé

12. Jeu de Cornhole (Labolycee Bac Mars 2021, Python)