|
Cours :
 
Activités expérimentales
Fiches méthodes
Puissances de
10, notation scientifique
 
Unités légales
du système international / conversion
 
Méthode de
résolution d’exercices
 
Résoudre une
équation à une inconnue
 
Programme officiel
|
Notions et contenus
|
Capacités exigibles
Activités
expérimentales support de la formation
|
|
Les transformations
nucléaires, introduites en classe de seconde, sont réinvesties dans
l’enseignement scientifique en classe de première où sont abordés, de
manière qualitative ou graphique, le caractère aléatoire de la
désintégration de noyaux radioactifs et la décroissance de l’activité d’un
échantillon. En classe terminale, il s’agit de passer de l’étude limitée au
cas de durées discrètes (multiples entiers du temps de demi-vie) à une loi
d’évolution d’une population de noyaux régie par une équation différentielle
linéaire du
premier ordre. Cette partie
permet de réinvestir la notion d’isotope, d’utiliser le diagramme (N,Z),
d’identifier le type de radioactivité et d’écrire des équations de réaction
de désintégration. Des applications peuvent être proposées dans les
domaines de l’archéologie, de la santé, de la médecine, du stockage des
substances radioactives, de la protection, etc.
Notions abordées en
classe de seconde (enseignement commun de physique-chimie) et de première
(enseignement scientifique) :
Composition du noyau d’un
atome, isotopes, transformation
nucléaire, aspects énergétiques des transformations nucléaires (Soleil,
centrales nucléaires), caractère aléatoire de la désintégration
radioactive, temps de demi-vie, datation, équivalence masse-énergie, fusion
de l’hydrogène dans les étoiles.
|
|
Décroissance radioactive
Stabilité et instabilité
des noyaux : diagramme (N,Z), radioactivité α et β, équation
d’une réaction nucléaire, lois de conservation.
Radioactivité .
|
Déterminer, à partir d’un
diagramme (N,Z), les isotopes radioactifs d’un élément.
Utiliser des données et les
lois de conservation pour écrire l’équation d’une réaction nucléaire et
identifier le type de radioactivité.
|
|
Évolution temporelle d’une
population de noyaux radioactifs ; constante radioactive ; loi de
décroissance radioactive ; temps de demi-vie ;
activité.
|
Établir l’expression de
l’évolution temporelle de la population de noyaux radioactifs.
Exploiter la loi et une
courbe de décroissance radioactive.
Capacité mathématique : Résoudre une équation différentielle linéaire du
premier ordre à coefficients constants.
|
|
Radioactivité naturelle ;
applications à la datation.
Applications dans le
domaine médical ; protection contre les rayonnements ionisants.
|
Expliquer le principe de la
datation à l’aide de noyaux radioactifs et dater un événement.
Citer quelques applications
de la radioactivité dans le domaine médical.
Citer des méthodes de
protection contre les rayonnements ionisants et des facteurs d’influence de
ces protections.
|
|
1.Datation
du carbone 14 (Ministère, correction vidéo))
3. Source radioactive de césium 137
(correction vidéo)
4.
Application technologique de la radioactivité (Asie 2003)
(correction vidéo)
5. l’âge de la
Terre (Antilles 2003)
6. déchets
radioactifs et synthèse organique (Antilles 2008)
|
Radioactivité
Diagramme de Segré
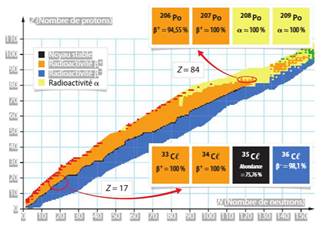
|
Nucléide et isotope
La radioactivité, loi de
conservation
La radioactivité alpha
Radioactivité
béta plus
Radioactivité gamma
Relation entre demi vie et constante de
désintégration : t1/2 = ln(2)/l
Datation
par le carbone 14

|






